
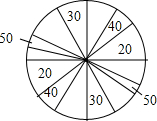
 某商场搞促销活动,规定凡购物满200元就有一次摇奖机会,摇奖的转盘如图所示.转盘上写有礼券金额,其中20元、30元、40元、50元礼券所对应的扇形的圆心角之和依次为80°、60°、40°、20°.计算:
某商场搞促销活动,规定凡购物满200元就有一次摇奖机会,摇奖的转盘如图所示.转盘上写有礼券金额,其中20元、30元、40元、50元礼券所对应的扇形的圆心角之和依次为80°、60°、40°、20°.计算:分析 (1)根据摇一次奖获得20元礼券对应的扇形的圆心角之和为80°即可得出结论;
(2)根据摇一次奖获得30元礼券对应的扇形的圆心角之和为60°即可得出结论;
(3)先求出所有礼券圆心角的和,再根据概率公式即可得出结论.
解答 解:(1)∵摇一次奖获得20元礼券对应的扇形的圆心角之和为80°,
∴摇一次奖获得20元礼券的概率=$\frac{80}{360}$=$\frac{2}{9}$;
(2)∵摇一次奖获得30元礼券对应的扇形的圆心角之和为60°,
∴摇一次奖获得礼券大于30元的概率=$\frac{60}{360}$=$\frac{1}{6}$;
(3)∵摇一次奖获得礼券所对应的扇形的圆心角之和为80°+60°+40°+20°=200°,
∴摇一次奖获得礼券的概率=$\frac{200}{360}$=$\frac{5}{9}$.
点评 本题考查的是概率公式,熟记随机事件A的概率P(A)=事件A可能出现的结果数所有可能出现的结果数的商是解答此题的关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C地,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发xh后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.
已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C地,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发xh后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
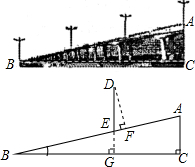 如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°.
如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com