
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,AD:BD=2:3,求BE的长.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连OD,OE,根据圆周角定理得到∠ADO+∠ODB=90°,而∠CDA=∠CBD,∠CBD=∠ODB,于是∠CDA+∠ADO=90°;
(2)根据已知条件得到△CDA∽△CBD由相似三角形的性质得到![]() ,求得CD=4,由切线的性质得到BE=DE,BE⊥BC根据勾股定理列方程即可得到结论.
,求得CD=4,由切线的性质得到BE=DE,BE⊥BC根据勾股定理列方程即可得到结论.
试题解析:(1)证明:连结OD,
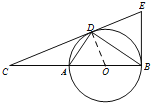
∵OB=OD,
∴∠OBD=∠BDO,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB,
又∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠ODB=90°,
∴∠ADO+∠CDA=90°,
即∠CDO=90°,
∴OD⊥CD,
∵OD是⊙O半径,
∴CD是⊙O的切线
(2)∵∠C=∠C,∠CDA=∠CBD
∴△CDA∽△CBD
∴![]()
∵![]() ,BC=6,
,BC=6,
∴CD=4,
∵CE,BE是⊙O的切线
∴BE=DE,BE⊥BC
∴BE2+BC2=EC2,即BE2+62=(4+BE)2
解得:BE=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,潜望镜中的两个镜片AB和CD是平行的,光线经过镜子反射时,∠AEN=∠BEF,∠EFD=∠CFM,那么进入潜望镜的光线NE和离开潜望镜的光线FM是平行的吗?说明理由.
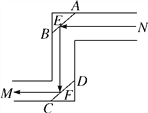
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家准备春节前举行80人的聚餐,需要去某餐馆订餐.据了解餐馆有10人坐和8人坐两种餐桌,要使所订的每个餐桌刚好坐满,则订餐方案共有______种.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶情况记录如下(单位:千米):+10,﹣8,+7,﹣15,+6,﹣16,+4,﹣2
(1)A处在岗亭何方?距离岗亭多远?
(2)若摩托车每行驶1千米耗油0.5升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县九年级有15000名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分(得分取正整数,满分100分)进行统计:
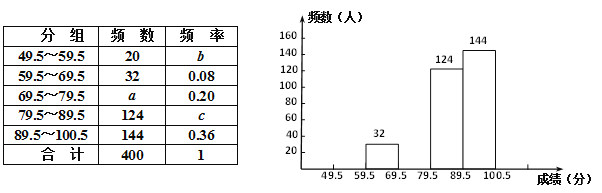
请结合图表完成下列问题:
(1)表中的![]() ,b= , c= ;
,b= , c= ;
(2)请把频数分布直方图补充完整;
(3)若将得分转化为等级,规定得分低于59.5分评为“D”,59.5~69.5分评为“C”,69.5~89.5分评为“B”,89.5~100.5分评为“A”,这次15000名学生中约有多少人被评为“B”?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com