
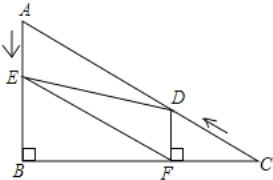
【题目】 如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点D从点C出发沿
.点D从点C出发沿![]() 方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿
方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿![]() 方向以每秒2个单位长的速度向点B匀速运动,设点D、E运动的时间是t秒
方向以每秒2个单位长的速度向点B匀速运动,设点D、E运动的时间是t秒![]() .过点D作
.过点D作![]() 于点F,连接
于点F,连接![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)四边形![]() 能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
【答案】(1)详见解析;(2)能,当![]() 时,四边形
时,四边形![]() 为菱形;(3)当
为菱形;(3)当![]() 或
或![]() 时,
时,![]() 为直角三角形,理由详见解析
为直角三角形,理由详见解析
【解析】
(1)由![]() ,
,![]() ,证出
,证出![]() ;
;
(2)先证明四边形![]() 为平行四边形.得出
为平行四边形.得出![]() ,
,![]() ,若
,若![]() 为等边三角形,则
为等边三角形,则![]() 为菱形,得出
为菱形,得出![]() ,
,![]() ,求出
,求出![]() ;
;
(3)分三种情况讨论:①![]() 时;②
时;②![]() 时;③
时;③![]() 时,第③种情况不存在;分别求出t的值即可.
时,第③种情况不存在;分别求出t的值即可.
解:(1)证明:在![]() 中,
中,![]() ,
,![]() ,
,![]()
![]()
又![]()
![]() ;
;
(2)能;
理由如下:
![]() ,
,
![]() .
.
又![]() ,
,
![]() 四边形
四边形![]() 为平行四边形.
为平行四边形.
![]() ,
,
![]()
![]()
![]() 平行四边形
平行四边形![]() 为菱形,则
为菱形,则![]()
![]() ,
,
![]()
即当![]() 时,四边形
时,四边形![]() 为菱形;
为菱形;
(3)当![]() 或
或![]() 时,
时,![]() 为直角三角形;
为直角三角形;
理由如下:
①![]() 时,四边形
时,四边形![]() 为矩形.
为矩形.
在![]() 中,
中,![]() ,
,
![]() .即
.即![]() ,
,
![]()
②![]() 时,由(2)知
时,由(2)知![]() ,
,
![]() .
.
![]()
![]()
即![]()
![]()
③![]() 时,
时,
![]() ,
,
![]() 点E运动到点B处,用了
点E运动到点B处,用了![]() 秒,
秒,
同时点D也运动![]() 秒钟,点D就和点A重合,
秒钟,点D就和点A重合,
点F也就和点B重合,
点![]() 不能构成三角形.
不能构成三角形.
此种情况不存在;
综上所述,当![]() 或
或![]() 时,△DEF为直角三角形.
时,△DEF为直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在一个纸箱中,装有红色、黄色、白色的塑料球共200个这些小球除颜色外其他都完全相同,将球充分摇匀后,从中随机摸出一个球,记下它的颜色后再放回箱中,不断重复这一过程,小明发现其中摸到白色球、黄色球的频率分别稳定在15%和45%,则这个纸箱中红色球的个数可能有( )
A. 30个 B. 80个 C. 90个 D. 120个
查看答案和解析>>
科目:初中数学 来源: 题型:
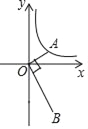
【题目】如图,已知点A是反比例y=![]() (x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为_____.
(x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
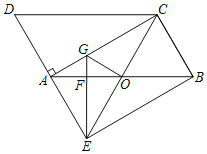
【题目】如图,在平行四边形ABCD中,![]() ,延长DA于点E,使得
,延长DA于点E,使得![]() ,连接BE.
,连接BE.
![]() 求证:四边形AEBC是矩形;
求证:四边形AEBC是矩形;
![]() 过点E作AB的垂线分别交AB,AC于点F,G,连接CE交AB于点O,连接OG,若
过点E作AB的垂线分别交AB,AC于点F,G,连接CE交AB于点O,连接OG,若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=﹣![]() +bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣
+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣![]() +bx+c的图象分别交于B,C两点,点B在第一象限.
+bx+c的图象分别交于B,C两点,点B在第一象限.
(1)求二次函数y=﹣![]() +bx+c的表达式;
+bx+c的表达式;
(2)连接AB,求AB的长;
(3)连接AC,M是线段AC的中点,将点B绕点M旋转180°得到点N,连接AN,CN,判断四边形ABCN的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
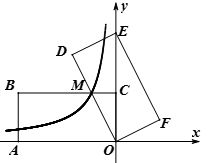
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在轴的负半轴、轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=![]() (x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=![]() ,,则BN的长为______________.
,,则BN的长为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中有3个大小相同的小球,球面上分别写有数字1,2,3,从袋中随机摸出一个小球,记录下数字后放回,再随机摸出一个小球.
(1)请用树状图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出球上的数字的积为奇数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com