
分析 (1)根据根的判别式,可得答案;
(2)根据根与系数的关系,可得A、B间的距离,根据二次函数的性质,可得答案.
解答 解:(1)△=[-(m-3)]2-4(-m)=m2-2m+9=(m-1)2+8,
∵(m-1)2≥0,
∴△=(m-1)2+8>0,
∴原方程有两个不等实数根;
(2)存在,
由题意知x1,x2是原方程的两根,
∴x1+x2=m-3,x1•x2=-m.
∵AB=|x1-x2|,
∴AB2=(x1-x2)2=(x1+x2)2-4x1x2
=(m-3)2-4(-m)=(m-1)2+8,
∴当m=1时,AB2有最小值8,
∴AB有最小值,即AB=$\sqrt{8}$=2$\sqrt{2}$
点评 本题考查了抛物线与x轴的交点,利用了根的判别式,根据根与系数的关系,利用完全平方公式得出二次函数是解题关键,又利用了二次函数的性质.


 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
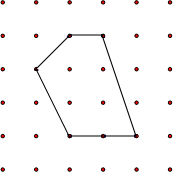 各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形.如何计算它的面积?奥地利数学家皮克(G•Pick,1859~1942年)证明了格点多边形的面积公式S=a+$\frac{1}{2}$b-1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图,a=4,b=6,S=4+$\frac{1}{2}$×6-1=6
各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形.如何计算它的面积?奥地利数学家皮克(G•Pick,1859~1942年)证明了格点多边形的面积公式S=a+$\frac{1}{2}$b-1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图,a=4,b=6,S=4+$\frac{1}{2}$×6-1=6查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
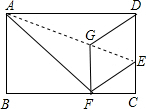 如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.
如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
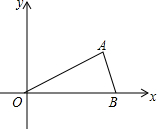 如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象经过点A.
如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象经过点A.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是50cm.
如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是50cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com