
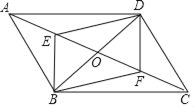
【题目】如图,ABCD的对角线AC、BD交于点O,E、F分别是AO、CO的中点,连接BE、DE、DF、BF,
(1)求证:四边形EBFD是平行四边形.
(2)求证:当AC=2BD时,四边形EBFD是矩形.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E在AB上,且D、E分别是AC、BC的垂直平分线上一点;若△CDE的周长为4,则AB的长为___________;若∠ACB=100°,则∠DCE=_________度; 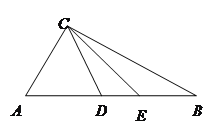
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图.
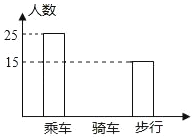
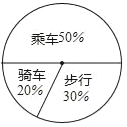
(1)求该班有多少名学生?
(2)补上骑车分布直方图的空缺部分;
(3)在扇形统计图中,求步行人数所占的圆心角度数;
(4)若全年级有900人,估计该年级骑车人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”.
(1)求函数y= ![]() x+2的图象上所有“中国结”的坐标;
x+2的图象上所有“中国结”的坐标;
(2)若函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(k≠0,k为常数)的图象上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(3)若二次函数y=(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k(k为常数)的图象与x轴相交得到两个不同的“中国结”,试问该函数的图象与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点A,B与正方形EFGH的顶点G,H同在一段抛物线上,且抛物线的顶点同时落在CD和y轴上,正方形边AB与EF同时落在x轴上,若正方形ABCD的边长为4,则正方形EFGH的边长为 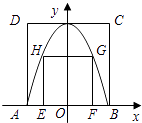
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
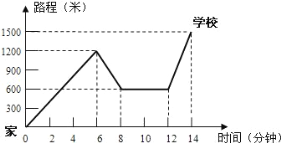
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读求绝对值不等式|x|<3和|x|>3的解集的过程:
因为|x|<3,从如图1所示的数轴上看:大于-3而小于3的数的绝对值是小于3的,所以|x|<3的解集是-3<x<3;
因为|x|>3,从如图2所示的数轴上看:小大于-3的数和大于3的数的绝对值是大于3的,所以|x|>3的解集是x<-3或x>3.
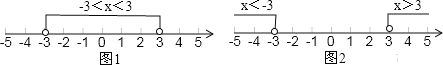
解答下面的问题:
(1)不等式|x|<a(a>0)的解集为______;不等式|x|>a(a>0)的解集为______.
(2)解不等式|x-5|<3;
(3)解不等式|x-3|>5.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系. 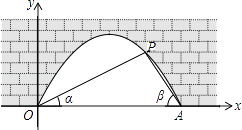
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com