
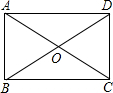
 如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AB=1,则AD的长为$\sqrt{3}$.
如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AB=1,则AD的长为$\sqrt{3}$.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
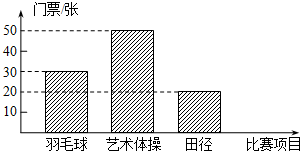 2010年5月20日上午10时起.2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分价格,如图为某公司购买的门票种类、数量所绘制的条形统计图.
2010年5月20日上午10时起.2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分价格,如图为某公司购买的门票种类、数量所绘制的条形统计图.| 比赛项目 | 票价(元/张) |
| 羽毛球 | 400 |
| 艺术体操 | 240 |
| 田径 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x$>\frac{3}{2}$ | B. | x$≥\frac{3}{2}$ | C. | x$<\frac{3}{2}$ | D. | x$≤\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
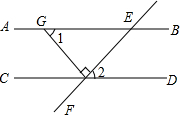 如图,AB∥CD,EF交AB、CD于点E、F,FG⊥EF交AB于点G,若∠1=50°,则∠2的度数是( )
如图,AB∥CD,EF交AB、CD于点E、F,FG⊥EF交AB于点G,若∠1=50°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 70° | D. | 140° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com