
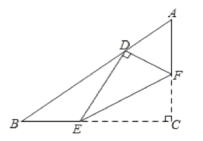
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则AD的长为___.
【答案】![]()
【解析】
△CEF与△ABC相似,分两种情况:①若CF:CE=3:4,此时EF∥AB,CD为AB边上的高;②若CE:CF=3:4,由相似三角形角之间的关系,可以推出∠B=∠ECD与∠A=∠FCD,从而得到CD=AD=BD,即D点为AB的中点.
若△CEF与△ABC相似,分两种情况:
①若CF:CE=3:4,
∵AC:BC=3:4,
∴CF:CE=AC:BC,
∴EF∥AB.
连接CD,如图1所示:

由折叠性质可知,CD⊥EF,
∴CD⊥AB,即此时CD为AB边上的高。
在Rt△ABC中,∵∠ACB=90°,AC=3,BC=4,
∴AB=![]() =5,
=5,
∴cosA=![]() ,
,
∴AD=ACcosA=3×![]() ;
;
②若CE:CF=3:4,
∵AC:BC=3:4,∠C=∠C,
∵△CEF∽△CAB,
∴∠CEF=∠A.
连接CD,如图2所示:

由折叠性质可知,∠CEF+∠ECD=90°,
又∵∠A+∠B=90°,
∴∠B=∠ECD,
∴BD=CD.
同理可得:∠A=∠FCD,AD=CD,
∴D点为AB的中点,
∴AD=![]() ;
;
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】函数![]() 的图象记为
的图象记为![]() ,函数
,函数![]() 的图象记为
的图象记为![]() ,其中
,其中![]() 为常数,
为常数,![]() 与
与![]() 合起来的图象记为
合起来的图象记为![]() .
.
(Ⅰ)若![]() 过点
过点![]() 时,求
时,求![]() 的值;
的值;
(Ⅱ)若![]() 的顶点在直线
的顶点在直线![]() 上,求
上,求![]() 的值;
的值;
(Ⅲ)设![]() 在
在![]() 上最高点的纵坐标为
上最高点的纵坐标为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
动手操作:
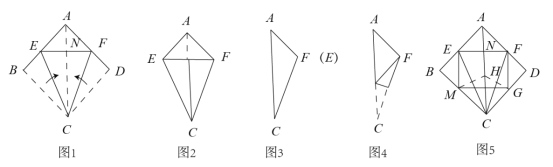
第一步:如图1,正方形纸片ABCD沿对角线AC所在直线折叠,展开铺平.在沿过点C的直线折叠,使点B,点D都落在对角线AC上.此时,点B与点D重合,记为点N,且点E,点N,点F三点在同一直线上,折痕分别为CE,CF.如图2.
第二步:再沿AC所在的直线折叠,△ACE与△ACF重合,得到图3
第三步:在图3的基础上继续折叠,使点C与点F重合,如图4,展开铺平,连接EF,FG,GM,ME,如图5,图中的虚线为折痕.
问题解决:
(1)在图5中,∠BEC的度数是 ,![]() 的值是 ;
的值是 ;
(2)在图5中,请判断四边形EMGF的形状,并说明理由;
(3)在不增加字母的条件下,请你以图中5中的字母表示的点为顶点,动手画出一个菱形(正方形除外),并写出这个菱形: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.
(1)求大本作业本与小本作业本每本各多少元?
(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AD、BD分别是△ABC的内角∠BAC、∠ABC的平分线,过点A作AE上AD,交BD的延长线于点E.
(1)求证:∠E=![]() ∠C;
∠C;
(2)如图2,如果AE=AB,且BD:DE=2:3,求cos∠ABC的值;
(3)如果∠ABC是锐角,且△ABC与△ADE相似,求∠ABC的度数,并直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
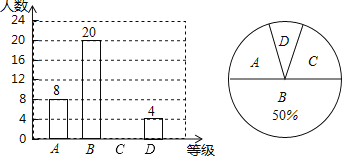
【题目】某企业为了解员工安全生产知识掌握情况,随机抽取了部分员工进行安全生产知识测试,测试试卷满分100分.测试成绩按A、B、C、D四个等级进行统计,并将统计结果绘制了如下两幅不完整的统计图.(说明:测试成绩取整数,A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
请解答下列问题:
(1)该企业员工中参加本次安全生产知识测试共有 人;
(2)补全条形统计图;
(3)若该企业共有员工800人,试估计该企业员工中对安全生产知识的掌握能达到A级的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BD为正方形ABCD的对角线,P、Q两点分别在AB、BD上,且满足∠PCQ=∠ABD.
(1)求:![]() 的值;
的值;
(2)由于四边形不具稳定性,把正方形ABCD沿D向右拉动,使∠BAD=120时,此时线段CD、DQ、BP有何数量关系,请说明理由.
(3)如图3,在(2)的条件下,延长CQ交AD边于点E交BA的延长线于点M,作∠DCE的平分线交AD边于点F,若CQ:PM=5:7,EF= a,求线段CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面图形![]() ,点
,点![]() 、
、![]() 是
是![]() 上任意两点,我们把线段
上任意两点,我们把线段![]() 的长度的最大值称为平面图形
的长度的最大值称为平面图形![]() 的“宽距”.例如,正方形的宽距等于它的对角线的长度.
的“宽距”.例如,正方形的宽距等于它的对角线的长度.
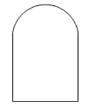
(1)写出下列图形的宽距:
①半径为![]() 的圆:________;
的圆:________;
②如图,上方是半径为![]() 的半圆,下方是正方形的三条边的“窗户形“:________;
的半圆,下方是正方形的三条边的“窗户形“:________;
(2)如图,在平面直角坐标系中,已知点![]() 、
、![]() ,
,![]() 是坐标平面内的点,连接
是坐标平面内的点,连接![]() 、
、![]() 、
、![]() 所形成的图形为
所形成的图形为![]() ,记
,记![]() 的宽距为
的宽距为![]() .
.
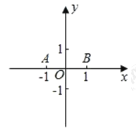
①若![]() ,用直尺和圆规画出点
,用直尺和圆规画出点![]() 所在的区域并求它的面积(所在区域用阴影表示);
所在的区域并求它的面积(所在区域用阴影表示);
②若点![]() 在⊙
在⊙![]() 上运动,⊙
上运动,⊙![]() 的半径为
的半径为![]() ,圆心
,圆心![]() 在过点
在过点![]() 且与
且与![]() 轴垂直的直线上.对于⊙
轴垂直的直线上.对于⊙![]() 上任意点
上任意点![]() ,都有
,都有![]() ,直接写出圆心
,直接写出圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com