
【题目】已知关于x的方程 ![]() +
+ ![]() =
= ![]() 恰有一个实根,则满足条件的实数a的值的个数为( ).
恰有一个实根,则满足条件的实数a的值的个数为( ).
A.1
B.2
C.3
D.4
【答案】B
【解析】先将原方程变形,转化为整式方程后得2x2﹣3x+(4﹣a)=0①.由于原方程只有一个实数根,因此,方程①的根有两种情况:(1)方程①有两个相等的实数根,此二等根使x(x﹣2)≠0;(2)方程①有两个不等的实数根,而其中一根使x(x﹣2)=0,另外一根使x(x﹣2)≠0.针对每一种情况,分别求出a的值及对应的原方程的根.
去分母,将原方程两边同乘x(x﹣2),整理得2x2﹣3x+(4﹣a)=0.①
方程①的根的情况有两种:
第一,方程①有两个相等的实数根,即△=9﹣4×2(4﹣a)=0.
解得a= ![]() .
.
当a= ![]() 时,解方程2x2﹣3x+(﹣
时,解方程2x2﹣3x+(﹣ ![]() +4)=0,得x1=
+4)=0,得x1= ![]() ,x2=
,x2= ![]() .
.
第二,方程①有两个不等的实数根,而其中一根使原方程分母为零,即方程①有一个根为0或2.
(i)当x=0时,代入①式得4﹣a=0,即a=4.
当a=4时,解方程2x2﹣3x=0,x(2x﹣3)=0,x1=0或x2=1.5.
而x1=0是增根,即这时方程①的另一个根是x=1.5.它不使分母为零,确是原方程的唯一根.
(ii)当x=2时,代入①式,得2×4﹣2×3+(4﹣a)=0,即a=6.
当a=6时,解方程2x2﹣3x+2=0,该方程无解.
因此,若原分式方程只有一个实数根时,所求的a的值分别是 ![]() ,4,共2个.
,4,共2个.
故选:B.
【考点精析】利用分式方程的解对题目进行判断即可得到答案,需要熟知分式方程无解(转化成整式方程来解,产生了增根;转化的整式方程无解);解的正负情况:先化为整式方程,求整式方程的解.


科目:初中数学 来源: 题型:
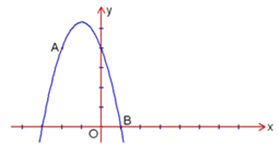
【题目】如图,已知点A(-2,4)和点B(1,0)都在抛物线![]() 上.
上.
(1)求![]() 、
、![]() ;
;
(2)向右平移上述抛物线,记平移后点A的对应点为![]() ,点B的对应点为
,点B的对应点为![]() ,若四边形
,若四边形![]() 为菱形,求平移后抛物线的表达式;
为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线![]() 的交点为C,试在
的交点为C,试在![]() 轴上找一个点D,使得以点
轴上找一个点D,使得以点![]() 、C、D为顶点的三角形与△ABC相似.
、C、D为顶点的三角形与△ABC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费.为更好地决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:

(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是按一定规律排列且形式相似的一列数: 第1个数:a1= ![]() ﹣(1+
﹣(1+ ![]() );
);
第2个数:a2= ![]() ﹣(1+
﹣(1+ ![]() )[1+
)[1+ ![]() ][1+
][1+ ![]() ]
]
第3个数:a3= ![]() ﹣(1+
﹣(1+ ![]() )[1+
)[1+ ![]() ][1+
][1+ ![]() ][1+
][1+ ![]() [1+
[1+ ![]() ]
]
(1)计算这三个数的结果(直接写答案): a1=;a2=;a3=;
(2)请按上述规律写出第4个数a4的形式并计算结果;
(3)请根据上述规律写出第n (n为正整数)个数an的形式(中间部分用省略号,两端部分必须写详细),然后直接写出计算结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“4000辆自行车、187个服务网点”,台州市区现已实现公共自行车服务全覆盖,为人们的生活带来了方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结沦中,错误的有( ) ①Rt△ABC中,已知两边分别为3和4,则第三边的长为5;
②三角形的三边分别为a、b、c , 若a2+b2=c2 , 则∠A=90°;
③若△ABC中,∠A:∠B:∠C=1:5:6,则这个三角形是一个直角三角形;
④若(x﹣y)2+M=(x+y)2成立,则M=4xy .
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com