
分析 按有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算;对于(6)中的式子分两组计算,利用乘法分配律的逆用进行计算.
解答 解:(1)(-1.8)+(+0.2)+(-1.7)+(0.1)+(+1.8)+(+1.4)
=-1.8+0.2-1.7+0.1+1.8+1.4
=-3.5+3.5
=0;
(2)$({-\frac{17}{4}})+({-\frac{10}{3}})+({+\frac{13}{3}})+({+\frac{11}{3}})$
=-$\frac{17}{4}$-$\frac{10}{3}$+$\frac{13}{3}+\frac{11}{3}$
=-$\frac{17}{4}$$+\frac{14}{3}$
=-$\frac{51}{12}$$+\frac{56}{12}$
=$\frac{5}{12}$;
(3)-(-2)2-3÷(-1)3+0×(-2)3
=-4-3÷(-1)+0
=-4+3
=-1;
(4)$({\frac{1}{2}-\frac{5}{9}+\frac{5}{6}-\frac{7}{12}})$×(-36)
=-$\frac{1}{2}×36$+$\frac{5}{9}×36$-$\frac{5}{6}×36$$+\frac{7}{12}×36$
=-18+20-30+21
=-48+41
=-7;
(5)$-{1^4}-(1-0.5)×\frac{1}{3}×[2-{(-3)^2}]$
=-1-$\frac{1}{2}×\frac{1}{3}×(-7)$
=-1+$\frac{7}{6}$
=$\frac{1}{6}$;
(6)$0.7×1\frac{4}{9}+2\frac{3}{4}×({-15})-0.7×({-\frac{5}{9}})-\frac{1}{4}×15$
=0.7×$\frac{13}{9}$+0.7×$\frac{5}{9}$-15×$\frac{11}{4}$-15×$\frac{1}{4}$
=0.7×$(\frac{13}{9}+\frac{5}{9})$-15×$(\frac{11}{4}+\frac{1}{4})$
=0.7×2-15×3
=1.4-45
=-43.6;
(7)-$\frac{4}{5}$×[(-$\frac{1}{2}$)÷(0.75-1)+(-2)5]
=-$\frac{4}{5}$×[-$\frac{1}{2}$÷(-0.25)-32]
=-$\frac{4}{5}$×[$\frac{1}{2}×4$-32]
=-$\frac{4}{5}$×(-30)
=24.
点评 本题考查了有理数的混合运算,注意运算顺序和符号;本题使用的运算技巧是:①转化法:一是将除法转化为乘法,二是将乘方转化为乘法,三是在乘除混合运算中,通常将小数转化为分数进行约分计算.②凑整法:在加减混合运算中,通常将和为零的两个数,分母相同的两个数,和为整数的两个数,乘积为整数的两个数分别结合为一组求解.③巧用运算律:在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
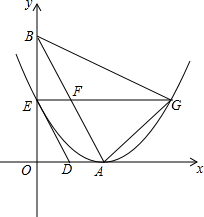 如图,直线y=-$\sqrt{3}$x+2$\sqrt{3}$与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和$\sqrt{3}$个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
如图,直线y=-$\sqrt{3}$x+2$\sqrt{3}$与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和$\sqrt{3}$个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2400名学生 | |
| B. | 100名学生 | |
| C. | 所抽取的100名学生对“白求恩同志事迹”的知晓情况 | |
| D. | 每一名学生对“白求恩同志事迹”的知晓情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形OABC的边OA,OC分别在y轴、x轴的正半轴,已知:A(0,4),B(4,3),C(4,0).
如图,四边形OABC的边OA,OC分别在y轴、x轴的正半轴,已知:A(0,4),B(4,3),C(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
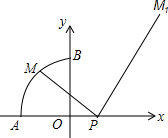 如图,点P(t,0)(t>0)是x轴正半轴上的一点,是以原点为圆心,半径为1的$\frac{1}{4}$圆,且A(-1,0),B(0,1),点M是$\widehat{AB}$上的一个动点,连结PM,作直角△MPM1,并使得∠MPM1=90°,∠PMM1=60°,我们称点M1为点M的对应点.
如图,点P(t,0)(t>0)是x轴正半轴上的一点,是以原点为圆心,半径为1的$\frac{1}{4}$圆,且A(-1,0),B(0,1),点M是$\widehat{AB}$上的一个动点,连结PM,作直角△MPM1,并使得∠MPM1=90°,∠PMM1=60°,我们称点M1为点M的对应点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com