
分析 设每本笔记本x元,每支圆珠笔y元,根据6本笔记本、5支圆珠笔共需80元;4本笔记本、8支圆珠笔共需72元,列方程组求解.
解答 解:设每本笔记本x元,每支圆珠笔y元,
由题意得,$\left\{\begin{array}{l}{6x+5y=80}\\{4x+8y=72}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=10}\\{y=4}\end{array}\right.$.
答:每本笔记本10元,每支圆珠笔4元.
点评 本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:填空题
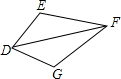 填空:如图,请你选择合适的条件填入空格中,使两个三角形全等.
填空:如图,请你选择合适的条件填入空格中,使两个三角形全等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
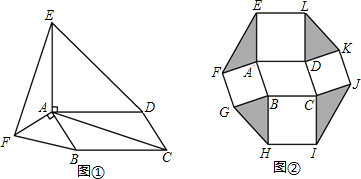
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
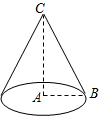 如图,已知在Rt△ABC中,∠BAC=90°,AC=4,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于( )
如图,已知在Rt△ABC中,∠BAC=90°,AC=4,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于( )| A. | 9π | B. | 12π | C. | 15π | D. | 20π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
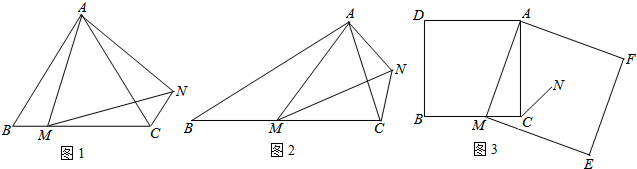
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com