
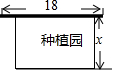
 成都市某学校计划建一个长方形种植园,如图所示,种植园的一边靠墙,另三边用周长为30m的篱笆围成,已知墙长为18m,设这个种植园垂直于墙的一边长为x(m),种植园面积为y(m2).
成都市某学校计划建一个长方形种植园,如图所示,种植园的一边靠墙,另三边用周长为30m的篱笆围成,已知墙长为18m,设这个种植园垂直于墙的一边长为x(m),种植园面积为y(m2).分析 (1)根据题意即可求得y与x的函数关系式为y=(30-2x)x;
(2)根据“种植园的面积不小于100m2”列出一元二次不等式,解之可得,根据二次函数的最值问题,即可求得这个苗圃园的面积最大值.
解答 解:(1)根据题意得:y=(30-2x)x=-2x2+30x,
(2)由题意得:-2x2+30x≥100,
解得:5≤x≤10,
∵30-2x≤18,
∴x≥6,
∴6≤x≤10,
∵y=-2x2+30x=-2(x-7.5)2+112.5,
∴当x=7.5时,这个种植园的面积的最大值,最大面积为112.5m2.
点评 此题考查了二次函数的实际应用问题.解题的关键是根据题意构建二次函数模型,然后根据二次函数的性质求解即可.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
 按要求完成下列各题:
按要求完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
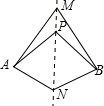 如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )| A. | AM=BM | B. | ∠ANM=∠BNM | C. | ∠MAP=∠MBP | D. | AP=BN |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{9}$ | C. | $\frac{1}{2}$ | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在正方形网格中,△ABC的位置如图所示,则tanB的值为( )
在正方形网格中,△ABC的位置如图所示,则tanB的值为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com