
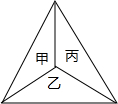
 如图,一只蚊子在甲、乙、丙三个房间之间飞来飞去,蚊子从一个房间随机飞到另一个房间,共飞三次.
如图,一只蚊子在甲、乙、丙三个房间之间飞来飞去,蚊子从一个房间随机飞到另一个房间,共飞三次.分析 (1)先画出树状图展示8种等可能的结果数,再找出蚊子回到甲房间的结果数,然后根据概率公式计算;
(2)由可得开始时蚊子在甲房间,经过三次飞行后,蚊子回到甲房间的概率最小,所以想使蚊子经过三次飞行后回到乙房间的概率最大,则蚊子最开始时不能在乙房间.
解答 解:(1)画树状图为: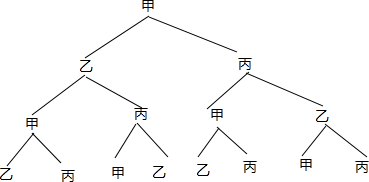
共有8种等可能的结果数,蚊子回到甲房间的结果数为2,
所以蚊子回到甲房间的概率=$\frac{2}{8}$=$\frac{1}{4}$;
(2)由(1)得开始时蚊子在甲房间,经过三次飞行后,蚊子回到乙或丙房间的概率都是$\frac{3}{8}$,
所有想使蚊子经过三次飞行后回到乙房间的概率最大,则蚊子最开始时在甲或丙房间.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3m-n}{n+m}$ | B. | -$\frac{3m-n}{n+m}$ | C. | $\frac{m-n}{m+n}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com