
【题目】如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.
求证: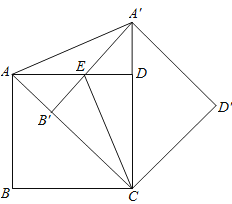
(1)△ADA′≌△CDE;
(2)直线CE是线段AA′的垂直平分线.
【答案】
(1)
证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠A′DE=90°,
根据旋转的方法可得:∠EA′D=45°,
∴∠A′ED=45°,
∴A′D=DE,
在△AA′D和△CED中
AD=CD
∠ADA′=∠EDC
A′D=ED∴△AA′D≌△CED(SAS);
(2)
证明:∵根据旋转可得AC=A′C,
∴点C在AA′的垂直平分线上,
∵AC是正方形ABCD的对角线,
∴∠CAE=45°,
∵AC=A′C,CD=CB′,
∴AB′=A′D,
在△AEB′和△A′ED中
∠EAB′=∠EA′D
∠AEB′=∠A′ED
AB′=A′D
∴△AEB′≌△A′ED,
∴AE=A′E,
∴点E也在AA′的垂直平分线上,
∴直线CE是线段AA′的垂直平分线
【解析】(1)根据正方形的性质可得AD=CD,∠ADC=90°,∠EA′D=45°,则∠A′DE=90°,再计算出∠A′ED=45°,根据等角对等边可得A′D=ED,即可利用SAS证明△AA′D≌△CED;(2)首先由AC=A′C,可得点C在AA′的垂直平分线上;再证明△AEB′≌△A′ED,可得AE=A′E,进而得到点E也在AA′的垂直平分线上,再根据两点确定一条直线可得直线CE是线段AA′的垂直平分线.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
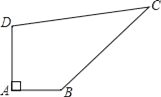
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形,第一个图2条直线相交最多有1个交点,第二个图3条直线相交最多有3个交点,第三个图4条直线相交最多有6个交点,…,像这样,则20条直线相交最多交点的个数是( )
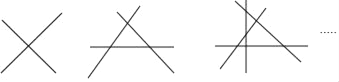
A. 171 B. 190 C. 210 D. 380
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是( )
A.45°
B.30°
C.25°
D.15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB,按下列要求完成画图和计算:
(1)延长线段AB到点C,使BC=2AB,取AC中点D;
(2)在(1)的条件下,如果AB=4,求线段BD的长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数 ![]() 是关于x的二次函数,求:
是关于x的二次函数,求:
(1)满足条件的k的值;
(2)当k为何值时,抛物线有最高点?求出这个最高点;
(3)当k为何值时,函数有最小值?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在 ![]() 上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )
上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )
A.![]()
![]()
B.![]()
![]()
C.2﹣ ![]()
![]()
D.2 ![]() ﹣2
﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8 …,顶点依次为A1,A2,A3,A4,A5,…,则顶点A55的坐标是( )

A. (13,13) B. (-13,-13) C. (-14,-14) D. (14,14)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com