
分析 由992=9801,前两位数99-1,后两位数是01;982=9604,前两位数98-2,后两位数是04;972=9409,前两位数97-3,后两位数是09;962=9216,前两位数96-4,后两位数是16;可以看出前两位是原数减去补数,后两位是原数的补数平方,用0凑两位数.
解答 解:∵992=9801,前两位数99-1,后两位数是01;
982=9604,前两位数98-2,后两位数是04;
972=9409,前两位数97-3,后两位数是09;
962=9216,前两位数96-4,后两位数是16;
∴这种平方速算的规律是:平方结果的四位数前两位数字是原数减去补数,后两位数字是补数的平方,位数不够四位时,用0凑位.
故答案为:平方结果的四位数前两位数字是原数减去补数,后两位数字是补数的平方,位数不够四位时,用0凑位.
点评 此题考查数字的变化规律,找出数字之间的联系,得出运算规律,解决问题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
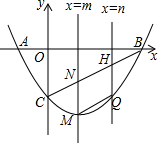 如图,在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线x=m(m>0),直线x=n(n>0)(m<n)分别交线段BC于N点、H点,交抛物线于M点、Q点.当NH∥MQ时,求m+n的值.
如图,在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线x=m(m>0),直线x=n(n>0)(m<n)分别交线段BC于N点、H点,交抛物线于M点、Q点.当NH∥MQ时,求m+n的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com