
【题目】如图,![]() 的对角线
的对角线![]() ,
,![]() 交于点
交于点![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() ,
,![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的是( )
.其中正确的是( )
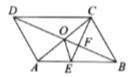
A.①②④B.①③④C.②③④D.①③
【答案】B
【解析】
根据三角形一边上的中线等于这边的一半则这个三角形是直角三角形对①进行判断;根据同高不等底的两个三角形面积的比是底的比对②进行判断;利用勾股定理及直角三角形中的![]() 角的性质进行计算求得
角的性质进行计算求得![]() 对③进行判断;根据平行线分线段成比例定理并利用中间比对④进行判断.
对③进行判断;根据平行线分线段成比例定理并利用中间比对④进行判断.
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=∠BCD =120°,
∵CE平分∠BCD交AB于点E,
∴∠DCE=∠BCE=60°
∴△CBE是等边三角形,
∴BE=BC=CE,
∵AB=2BC,
∴AE=BC=CE,
∴∠ACB=90°,
∵四边形ABCD是平行四边形,
∴![]() ,又∵AE= BE
,又∵AE= BE
∴OE是![]() 的中位线,
的中位线,
∴OE∥BC,
∴EO⊥AC,故①正确;
∵OE是![]() 的中位线,
的中位线,
∴OE∥BC,BC=2OE,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵由![]() 和
和![]() 同高不等底,
同高不等底,
∴![]() ,
,
∴![]() ,故②错误;
,故②错误;
在![]() 中,∠ACB=90°,∠CAB=30°,
中,∠ACB=90°,∠CAB=30°,
设![]() ,则
,则![]()
∴![]()
∴![]()
在![]() 中,∠OCB=90°,
中,∠OCB=90°,
∴![]()
∴![]()
∴![]() ,故③正确;
,故③正确;
∵OE∥BC,
∴![]() ,
,
∵BE∥DC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,故④正确;
,故④正确;
综上:①③④正确,
故选:B


科目:初中数学 来源: 题型:
【题目】下列两个三角形不一定相似的是
A.两条直角边的比都是![]() 的两个直角三角形
的两个直角三角形
B.腰与底的比都是![]() 的两个等腰三角形
的两个等腰三角形
C.有一个内角为![]() 的两个直角三角形
的两个直角三角形
D.有一个内角为![]() 的两个等腰三角形
的两个等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上的一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则下列结论中:

①![]() ;②
;②![]() ;③tan∠EAF=
;③tan∠EAF=![]() ;④
;④![]() 正确的是()
正确的是()
A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,经市场调查发现:该商品的月销售量y(件)是售价x(元/件)的一次函数,其售价x、月销售量y、月销售利润w(元)的部分对应值如下表:
售价x(元/件) | 40 | 45 |
月销售量y(件) | 300 | 250 |
月销售利润w(元) | 3000 | 3750 |
注:月销售利润=月销售量×(售价-进价)
(1)①求y关于x的函数表达式;
②当该商品的售价是多少元时,月销售利润最大?并求出最大利润;
(2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过40元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是2400元,则m的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
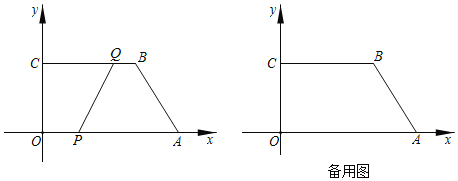
【题目】如图,在平面直角坐标系中,四边形![]() 的顶点坐标分别为
的顶点坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿边
个单位长度的速度沿边![]() 向终点
向终点![]() 运动;动点
运动;动点![]() 从点
从点![]() 同时出发,以每秒1个单位长度的速度沿边
同时出发,以每秒1个单位长度的速度沿边![]() 向终点
向终点![]() 运动,设运动的时间为
运动,设运动的时间为![]() 秒,
秒,![]() .
.
(1)直接写出![]() 关于
关于![]() 的函数解析式及
的函数解析式及![]() 的取值范围:_______;
的取值范围:_______;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)连接![]() 交
交![]() 于点
于点![]() ,若双曲线
,若双曲线![]() 经过点
经过点![]() ,问
,问![]() 的值是否变化?若不变化,请求出
的值是否变化?若不变化,请求出![]() 的值;若变化,请说明理由.
的值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运动会期间,甲、乙、丙三位同学参加乒乓球单打比赛,用抽签的方式确定第一场比赛的人选.
(1)若已确定甲参加第一次比赛,求另一位选手恰好是乙同学的概率;
(2)用画树状图或列表的方法,写出参加第一场比赛选手的所有可能,并求选中乙、丙两位同学参加第一场比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC 中,点 D 是线段 BC 上一点.作射线 AD ,点 B 关于射线 AD 的对称点为 E .连接 EC 并延长,交射线 AD 于点 F .

(1)补全图形;(2)求∠AFE 的度数;(3)用等式表示线段 AF 、CF 、 EF 之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com