
【题目】如图,已知数轴上点A表示的数为﹣6,点B在数轴上A点右侧,且AB=14,动点M从点A出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
![]()
(1)写出数轴上点B表示的数 ,点M表示的数 (用含t的式子表示);
(2)动点N从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点M,N同时出发,问点M运动多少秒时追上点N?
(3)若P为AM的中点,F为MB的中点,点M在运动过程中,线段PF的长度是否发生变化?若变化,请说明理由;若不变,请求出线段PF的长.
【答案】(1)8,5t﹣6;(2)点M运动7秒时追上点N;(3)线段PF的长度不发生变化,PF的长为:7.
【解析】
(1)根据点A表示的数,结合AB与AM的长,即可求解;
(2)设点M运动t秒时追上点N,列出关于t的方程,即可求解;
(3)根据点A,M,B在数轴上表示的数,P为AM的中点,F为MB的中点,进而得出点P,F表示的数,即可求解.
(1)∵AB=14,
∴点B表示的数为:14﹣6=8,
∵MA=5t,
∴点M表示的数为5t﹣6,
故答案为:8,5t﹣6;
(2)设点M运动t秒时追上点N,
∴5t=3t+14,
解得:t=7,
答:点M运动7秒时追上点N;
(3)∵点M表示的数为:5t﹣6,P为AM的中点,F为MB的中点,
∴点P表示的数为:![]() ,点F表示的数为:
,点F表示的数为:![]() ,
,
∴PF=![]() =7,
=7,
∴线段PF的长度不发生变化,PF的长为:7.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】下列命题正确的有( )
①如果等腰三角形的底角为15°,那么腰上的高是腰长的一半;
②三角形至少有一个内角不大于60°;
③连结任意四边形各边中点形成的新四边形是平行四边形;
④十边形内角和为1800°.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.

(1)如图1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;
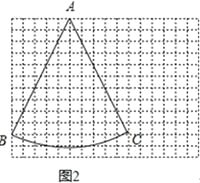
(2)如图2,在12×16的网格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C均在格点上,请在答题卷给出的两个网格图上各找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;
(3)四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
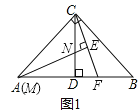
【题目】如图:已知△ABC中,CA=CB,CD⊥AB于D点,点M为线段AC上一动点,线段MN交DC于点N,且∠BAC=2∠CMN,过点C作CE⊥MN交MN延长线于点E,交线段AB于点F,探索![]() 的值.
的值.
(1)若∠ACB=90°,点M与点A重合(如图1)时:①线段CE与EF之间的数量关系是 ;②![]() = ;
= ;
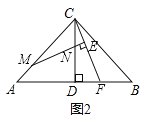
(2)在(1)的条件下,若点M不与点A重合(如图2),请猜想写出![]() 的值,并证明你的猜想
的值,并证明你的猜想
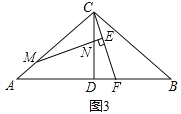
(3)若∠ACB≠90°,∠CAB=![]() ,其他条件不变,请直接写出
,其他条件不变,请直接写出![]() 的值(用含有
的值(用含有![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
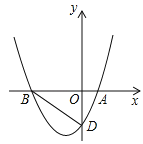
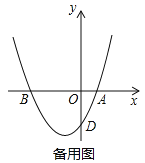
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2+bx+c的图象与x轴交于点A(2,0)、B(﹣4,0),与y轴交于点D.
x2+bx+c的图象与x轴交于点A(2,0)、B(﹣4,0),与y轴交于点D.
(1)求抛物线的解析式;
(2)连接BD,点P在抛物线的对称轴上,以Q为平面内一点,四边形PBQD能否成为矩形?若能,请求出点P的坐标;若不能,请说明理由;
(3)在抛物线上有一点M,过点M、A的直线MA交y轴于点C,连接BC,若∠MBO=∠BCO,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
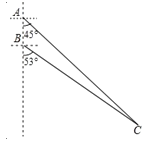
【题目】如图所示,我国两艘海监船 A,B 在南海海域巡逻,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船 C,此时,B 船在A 船的正南方向 15 海里处,A 船测得渔船 C 在其南偏东 45°方向,B 船测得渔船 C 在其南偏东 53°方向,已知 A 船的航速为 30 海里/小时,B 船的航速为 25 海里/小时,问 C 船至少要等待多长时间才能得到救援?(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈ 4 ,
,tan53°≈ 4 ,![]() 1.41 )
1.41 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】

A.12 B. 24 C. 12![]() D. 16
D. 16![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
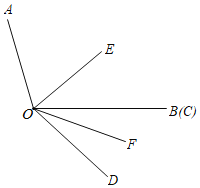
【题目】已知∠AOB=110°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.
(1)如图,求∠EOF的度数.
(2)如图,当OB、OC重合时,求∠AOE﹣∠BOF的值;
(3)当∠COD从图的位置绕点O以每秒3°的速度顺时针旋转t秒(0<t<10);在旋转过程中∠AOE﹣∠BOF的值是否会因t的变化而变化,若不发生变化,请求出该定值;若发生变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com