
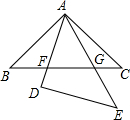
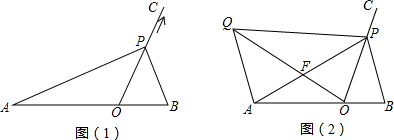
 ��ͼ��ABC���DEA������ȫ�ȵĵ���ֱ�������Σ���BAC=��D=90�㣬��DEA �Ƶ�A��ת����AD��AE��BC�ֱ���AD��AE�ཻ�ڵ�F��G��CB=5��
��ͼ��ABC���DEA������ȫ�ȵĵ���ֱ�������Σ���BAC=��D=90�㣬��DEA �Ƶ�A��ת����AD��AE��BC�ֱ���AD��AE�ཻ�ڵ�F��G��CB=5������ ��1�����ݵ���ֱ�������ε����ʵõ���C=��B=��DAE=��E=45�㣬����ǵ����ʵõ���CFA=��B+��FAB����GAB=��FAG+��FAB�����ǵõ���CFA=��BAG�����ɵõ����ۣ�
��2������ͬ��1��֤�á�AGF�ס�ACF���������������ε����ʼ��ɵõ����ۣ�
��3���ɡ�GAF�ס�GBA���ɵ�AG2=FG•BG������AF2=FG•FC����y=AF2+AG2=FG•��CB+FG�����̶����y��x�ĺ�����ϵʽ��
��4�����Ȱѡ�ABF��ת����ACP���á�ABF�ա�ACP��������������ȫ�ȵ�֪ʶ֤����ACP+��ACB=90�㣬��������֤��BF��FG��GC֮��Ĺ�ϵ��
��� ֤������1���ߡ�ABC���DEA������ȫ�ȵĵ���ֱ�������Σ���BAC=��EDA=90�㣬
���C=��B=��DAE=��E=45�㣬
�ߡ�CFA=��B+��FAB����GAB=��FAG+��FAB��
���CFA=��BAG��
���GAF�ס�GBA��
��2���ߡ�ABC���DEA������ȫ�ȵĵ���ֱ�������Σ���BAC=��EDA=90�㣬
���C=��B=��DAE=��E=45�㣬
�ߡ�FGA=��B+��EAC����CAF=��FAG+��EAC��
���AGF=��CAF��
���AGF�ס�ACF��
��$\frac{AF}{FG}=\frac{CF}{AF}$��
��AF2=FG•FC��
��3���ߡ�GAF�ס�GBA��
��$\frac{AG}{BG}=\frac{FG}{AG}$��
��AG2=FG•BG��
��AF2=FG•FC��
��y=AF2+AG2=FG•BG+FG•FC=FG•��BG+FC��=FG•��CB+FG����
��FG=x��CB=5��
��y=x��x+5��=x2+5x��
��4���ѡ�ABF��ת����ACP���á�ABF�ա�ACP��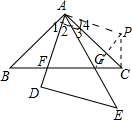
���1=��4��AF=AP��CP=BF����ACP=��B��
�ߡ�1+��3=45�㣬
���4+��3=45�㣬
���2=��4+��3=45�㣬
���2=��PAG��
�ڡ�FAG�͡�PAG�У�
$\left\{\begin{array}{l}{AF=AP}\\{��2=��PAG}\\{AG=AG}\end{array}\right.$��
���AFG�ա�AGP��SAS����
��FG=GP��
�ߡ�ACP+��ACB=45��+45��=90�㣬
����Rt��PGC��GP2=GC2+CP2��
��FG2=BF2+GC2��
���� �����������������ε��ۺ��⣮���������������ε��ж������ʡ�ȫ�������ε��ж������ʡ���ת�������Լ�����ֱ�����������ʣ�ע��ȷ�����������ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
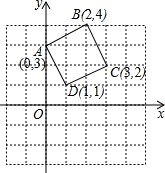 ������ABCD������ϵ�е�λ����ͼ��ʾ����������ABCD��D��˳ʱ�뷽����ת90���B�������Ϊ��4��0������DCBɨ�������Ϊ$\frac{5}{2}$��+$\frac{5}{2}$��
������ABCD������ϵ�е�λ����ͼ��ʾ����������ABCD��D��˳ʱ�뷽����ת90���B�������Ϊ��4��0������DCBɨ�������Ϊ$\frac{5}{2}$��+$\frac{5}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
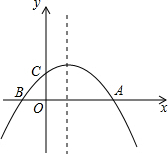 ��ͼ����֪������y=-$\frac{1}{a}$��x+2����x-a����a��0����x�ύ�ڵ�A��B����A�ڵ�B�Ҳࣩ����y�ύ�ڵ�C�������߹���N��6��һ4����
��ͼ����֪������y=-$\frac{1}{a}$��x+2����x-a����a��0����x�ύ�ڵ�A��B����A�ڵ�B�Ҳࣩ����y�ύ�ڵ�C�������߹���N��6��һ4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC���ACB��ƽ���߽���I������ABC+��ACB=130�㣬���BIC=115�㣮
��ͼ����ABC���ACB��ƽ���߽���I������ABC+��ACB=130�㣬���BIC=115�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ԡ�ABC������AB��ACΪ�ױ�����������ֱ��������ADB��ACE������DE����S��ADE��S�ı���DBCE=1��2����tan��AED=$\frac{3}{4}$����$\frac{AB}{AC}$��ֵΪ$\frac{\sqrt{34}}{5}$��
��ͼ���ԡ�ABC������AB��ACΪ�ױ�����������ֱ��������ADB��ACE������DE����S��ADE��S�ı���DBCE=1��2����tan��AED=$\frac{3}{4}$����$\frac{AB}{AC}$��ֵΪ$\frac{\sqrt{34}}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com