
【题目】如图,![]() 中,
中,![]() ,
,![]() 、
、![]() 分别平分
分别平分![]() ,
,![]() ,则
,则![]() ________,若
________,若![]() 、
、![]() 分别平分
分别平分![]() ,
,![]() 的外角平分线,则
的外角平分线,则![]() ________.
________.

【答案】![]()
![]()
【解析】
首先根据三角形内角和求出∠ABC+∠ACB的度数,再根据角平分线的性质得到∠IBC=![]() ∠ABC,∠ICB=
∠ABC,∠ICB=![]() ∠ACB,求出∠IBC+∠ICB的度数,再次根据三角形内角和求出∠I的度数即可;
∠ACB,求出∠IBC+∠ICB的度数,再次根据三角形内角和求出∠I的度数即可;
根据∠ABC+∠ACB的度数,算出∠DBC+∠ECB的度数,然后再利用角平分线的性质得到∠1=![]() ∠DBC,∠2=
∠DBC,∠2=![]() ECB,可得到∠1+∠2的度数,最后再利用三角形内角和定理计算出∠M的度数.
ECB,可得到∠1+∠2的度数,最后再利用三角形内角和定理计算出∠M的度数.
∵∠A=100°.
∵∠ABC+∠ACB=180°﹣100°=80°.
∵BI、CI分别平分∠ABC,∠ACB,∴∠IBC=![]() ∠ABC,∠ICB=
∠ABC,∠ICB=![]() ∠ACB,∴∠IBC+∠ICB=
∠ACB,∴∠IBC+∠ICB=![]() ∠ABC+
∠ABC+![]() ∠ACB=
∠ACB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×80°=40°,∴∠I=180°﹣(∠IBC+∠ICB)=180°﹣40°=140°;
×80°=40°,∴∠I=180°﹣(∠IBC+∠ICB)=180°﹣40°=140°;
∵∠ABC+∠ACB=80°,∴∠DBC+∠ECB=180°﹣∠ABC+180°﹣∠ACB=360°﹣(∠ABC+∠ACB)=360°﹣80°=280°.
∵BM、CM分别平分∠ABC,∠ACB的外角平分线,∴∠1=![]() ∠DBC,∠2=
∠DBC,∠2=![]() ECB,∴∠1+∠2=
ECB,∴∠1+∠2=![]() ×280°=140°,∴∠M=180°﹣∠1﹣∠2=40°.
×280°=140°,∴∠M=180°﹣∠1﹣∠2=40°.
故答案为:140°;40°.


科目:初中数学 来源: 题型:
【题目】如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.
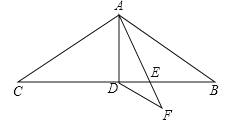
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°.
(1)△ACD是直角三角形吗?为什么?
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?
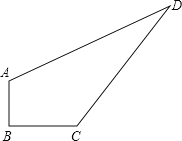
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四个命题:①全等三角形的面积相等;②最小角等于50°的三角形是锐角三角形;③等腰△ABC中,D是底边BC上一点,E是一腰AC上的一点,若∠BAD=60°且AD=AE,则∠EDC=30°;④将多项式![]() 因式分解,其结果为-y(2x+1)(x-3).其中正确命题的序号为___________.
因式分解,其结果为-y(2x+1)(x-3).其中正确命题的序号为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某抛物线的对称轴为直线x=2,点E是该抛物线顶点,抛物线与y轴交于点C,过点C作CD∥x轴,与抛物线交于点B,与对称轴交于点D,点A是对称轴上一点,连结AC,AB,若△ABC是等边三角形,则图中阴影部分图形的面积之和是 . 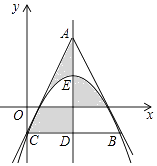
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E分别为AB、AC上的点,∠BDE、∠CED的平分线分别交BC于点F、G,EG∥AB.若∠BGE=110°,则∠BDF的度数为___________
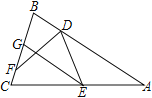
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是 ( )

A. ![]() B.
B. ![]() C. 6 D. 3
C. 6 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com