
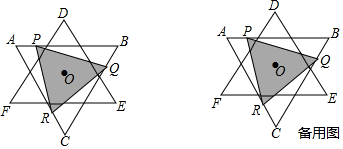
分析 (1)根据△ABC与△DEF所构成的图形既是轴对称图形,又是中心对称图形,可得△DEF可由△ABC绕O点顺时针旋转60°得到;
(2)①由对称性可得△APR≌△BQP≌△CRQ,进而得到S△PRQ=S△ABC-3S△APR,根据${S_{△PRQ}}=\frac{{3\sqrt{3}}}{4}{x^2}-\frac{{9\sqrt{3}}}{4}x+\frac{{9\sqrt{3}}}{4}=\frac{{3\sqrt{3}}}{4}{({x-\frac{3}{2}})^2}+\frac{{9\sqrt{3}}}{16}({0≤x≤3})$,可得当$x=\frac{3}{2}$时,△PQR面积最小,最小值为$\frac{{9\sqrt{3}}}{16}$;
②分三种情况讨论:当0≤x≤1时,当1≤x≤2时,当2≤x≤3时,分别根据△PQR与△DEF重合部分的面积为S,用含x的代数式表示S即可.
解答 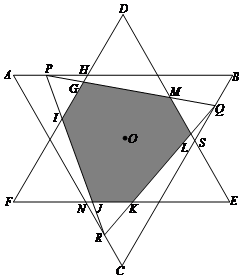 解:(1)将△ABC绕O点顺时针旋转60°;
解:(1)将△ABC绕O点顺时针旋转60°;
(2)①由对称性可得△APR≌△BQP≌△CRQ,
∴S△PRQ=S△ABC-3S△APR,
∵${S_{△ABC}}=\frac{1}{2}×3×3×\frac{{\sqrt{3}}}{2}=\frac{{9\sqrt{3}}}{2}$,${S_{△APR}}=\frac{1}{2}x({3-x})×\frac{{\sqrt{3}}}{2}=-\frac{{\sqrt{3}}}{4}{x^2}+\frac{{3\sqrt{3}}}{4}x$,
∴${S_{△PRQ}}=\frac{{3\sqrt{3}}}{4}{x^2}-\frac{{9\sqrt{3}}}{4}x+\frac{{9\sqrt{3}}}{4}=\frac{{3\sqrt{3}}}{4}{({x-\frac{3}{2}})^2}+\frac{{9\sqrt{3}}}{16}({0≤x≤3})$,
∴当$x=\frac{3}{2}$时,△PQR面积最小,最小值为$\frac{{9\sqrt{3}}}{16}$;
②Ⅰ.如上图,当0≤x≤1时,由对称性可得△DFM≌△ELK≌△FJI,
∴S=S△DEF-3S△DGM,
∵AP=BQ=CR=x,
∴PH=QS=RN=1-x,PB=3-x,
∵$\frac{HG}{BQ}=\frac{PH}{PB}$,
∴$HG=\frac{{x({1-x})}}{3-x}$,
∴$NJ=HG=\frac{{x({1-x})}}{3-x}$,
∴$DG=FJ=1+\frac{{x({1-x})}}{3-x}=\frac{{3-{x^2}}}{3-x}$,
∵$\frac{PH}{JF}=\frac{HI}{FI}$,且HF=2,
∴$FI=\frac{{3-{x^2}}}{3-2x}$,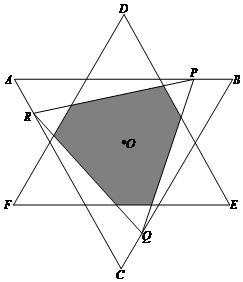
∴$DM=FI=\frac{{3-{x^2}}}{3-2x}$,
∴${S_{△DGM}}=\frac{1}{2}×\frac{{3-{x^2}}}{3-x}×\frac{{3-{x^2}}}{3-2x}×\frac{{\sqrt{3}}}{2}=\frac{{\sqrt{3}{{({{x^2}-3})}^2}}}{{4({x-3})({2x-3})}}$,
∵${S_{△DEF}}=\frac{1}{2}×3×3×\frac{{\sqrt{3}}}{2}=\frac{{9\sqrt{3}}}{4}$,
∴$S=\frac{{9\sqrt{3}}}{4}-\frac{{3\sqrt{3}{{({{x^2}-3})}^2}}}{{4({x-3})({2x-3})}}({0≤x≤1})$;
Ⅱ.当1≤x≤2时,重合部分面积即为△PQR的面积,
∴$S=\frac{{3\sqrt{3}}}{4}{x^2}-\frac{{9\sqrt{3}}}{4}x+\frac{{9\sqrt{3}}}{4}=\frac{{3\sqrt{3}}}{4}{({x-\frac{3}{2}})^2}+\frac{{9\sqrt{3}}}{16}({1≤x≤2})$;
Ⅲ.当2≤x≤3时,如右图,与0≤x≤1呈对称形,仅需将x替换为3-x即可,
∴$S=\frac{{9\sqrt{3}}}{4}-\frac{{3\sqrt{3}{{[{{{({3-x})}^2}-3}]}^2}}}{{4({3-x-3})({6-2x-3})}}=\frac{{9\sqrt{3}}}{4}-\frac{{3\sqrt{3}{{({{x^2}-6x+6})}^2}}}{{4x({2x-3})}}({2≤x≤3})$.
点评 本题属于三角形综合题,主要考查了中心对称图形的性质,等边三角形的性质以及二次函数的最值的综合应用,解决问题的关键是根据图形进行分类讨论.确定一个二次函数的最值,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标.


科目:初中数学 来源: 题型:选择题
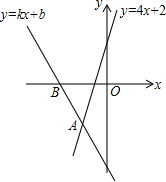 如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b的解集为( )
如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b的解集为( )| A. | x<-2 | B. | x>-1 | C. | x<-1 | D. | x>-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com