
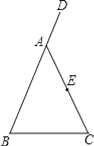
【题目】如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
(1)利用尺规作出∠DAC的平分线AM,连接BE并延长交AM于点F,(要求在图中标明相应字母,保留作图痕迹,不写作法);
(2)试判断AF与BC有怎样的位置关系与数量关系,并说明理由.
【答案】(1)作图见解析;(2)AF∥BC且AF=BC,理由见解析.
【解析】试题分析:(1)根据题意画出图形即可;
(2)根据等腰三角形的性质,可得两底角相等,根据三角形的外角的性质,可得∠DAC=∠ABC+∠C,根据内错角相等,可得两直线平行,根据ASA,可得两个三角形全等,根据全等三角形的性质,可得证明结论.
试题解析:(1)如图:
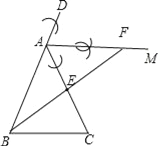
(2)AF∥BC且AF=BC,理由如下:
∵AB=AC,∴∠ABC=∠C,
∵∠DAC=∠ABC+∠C,∴∠DAC=2∠C,
由作图可知∠DAC=2∠FAC,∴∠C=∠FAC,∴AF∥BC;
∵E是AC的中点,∴AE=CE,
在△AEF和△CEB中, 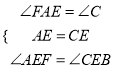 ,∴△AEF≌△CEB (ASA),
,∴△AEF≌△CEB (ASA),
∴AF=BC.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
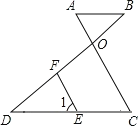
【题目】如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:FE∥OC;
(2)若∠BOC比∠DFE大20,求∠OFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
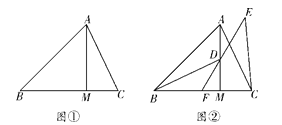
【题目】在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.
(1)如图①,若AB=3![]() ,BC=5,求AC的长;
,BC=5,求AC的长;
(2)如图②,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,已知直线![]() 和双曲线
和双曲线![]() (k>0),点A(m,n)在双曲线
(k>0),点A(m,n)在双曲线 ![]() 上.当m=n=2时.
上.当m=n=2时.
(1)直接写出k的值;
(2)将直线![]() 作怎样的平移能使平移后的直线与双曲线
作怎样的平移能使平移后的直线与双曲线 ![]() 只有一个交点.
只有一个交点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)抛物线![]() 经过点A (4,0),点B (1,-3) ,求该抛物线的解析式;
经过点A (4,0),点B (1,-3) ,求该抛物线的解析式;
(2)如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?

(3)如图,点P![]() (
(![]() >0),在
>0),在![]() 轴正半轴上,过点P作平行于
轴正半轴上,过点P作平行于![]() 轴的直线,分别交抛物线
轴的直线,分别交抛物线![]() 于点A,B,交抛物线
于点A,B,交抛物线![]() 于点C,D,求
于点C,D,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
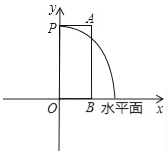
【题目】某市人民广场上要建一个圆形的喷水池,并在水池中央垂直安装一个柱子OP,柱子顶端P处装上喷头,由P处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示).若已知OP=3米,喷出的水流的最高点A距水平面的高度是4米,离柱子OP的距离为1米.
(1)求这条抛物线的解析式;
(2)若不计其它因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com