
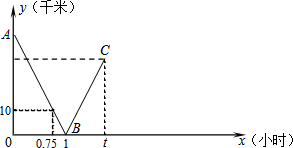
 С����С�������ﳵ��ƽֱ�Ĺ�·�Ϸֱ�Ӽס�������������У�����ͬʱ������������ʻ������ʻ��ʱ��Ϊx��ʱ��������֮��ľ���Ϊy��ǧ�ף���С�������ҵغ����̷��ؼأ�С������غ�ֹͣ��ʻ��ͼ�е����߱�ʾ�����˳�����С�������ҵع�����y��x֮��ĺ�����ϵ��
С����С�������ﳵ��ƽֱ�Ĺ�·�Ϸֱ�Ӽס�������������У�����ͬʱ������������ʻ������ʻ��ʱ��Ϊx��ʱ��������֮��ľ���Ϊy��ǧ�ף���С�������ҵغ����̷��ؼأ�С������غ�ֹͣ��ʻ��ͼ�е����߱�ʾ�����˳�����С�������ҵع�����y��x֮��ĺ�����ϵ������ ��1�����ݴ���ϵ�����ó�һ�κ����Ľ���ʽ��ɣ�
��2����С�����ٶ�Ϊmǧ��/ʱ��С�����ٶ�Ϊnǧ��/ʱ�����������г��������ɣ�
��3����������Ի���ͼ�ɣ�
��� �⣺��1����ֱ��ABΪ��y=kx+b��
��ͼ���֪$\left\{\begin{array}{l}0=k+b\\ 10=0.75k+b.\end{array}\right.$����ã�$\left\{\begin{array}{l}k=-40\\ b=40.\end{array}\right.$��
���������֮��ľ���40ǧ�ף�
��2����С�����ٶ�Ϊmǧ��/ʱ��С�����ٶ�Ϊnǧ��/ʱ��������ã�$\left\{\begin{array}{l}m+n=40\\ m-n=4\end{array}\right.$����ã�$\left\{\begin{array}{l}m=22\\ n=18\end{array}\right.$��
��С�����ٶ�Ϊ22ǧ��/ʱ��
��$t=\frac{40}{22}=\frac{20}{11}$�� ������
��3����ͼ��ʾ��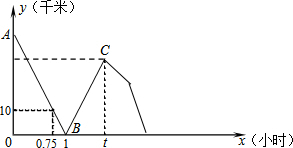
���� ���⿼�������ô���ϵ������һ�κ����Ľ���ʽ�����ã��г������������ϵ�����ã�һԪһ�η��̵����ã�������ͼ������ã����ʱ���һ�κ����Ľ���ʽ�ǹؼ���


 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �����죬Сǿ��ѧУ����ȥͼ��ݣ�ͬʱ���ȵ�ͼ��ݵ�С���ﳵ��Уȡ������ѧ�������õ�������;������Сǿ��Сǿ����������ͼ��ݣ���ͼ�������뿪ͼ��ݵľ���y���ף������ʱ��x���֣�֮��ĺ���ͼ����ͼ����Ϣ������⣺
�����죬Сǿ��ѧУ����ȥͼ��ݣ�ͬʱ���ȵ�ͼ��ݵ�С���ﳵ��Уȡ������ѧ�������õ�������;������Сǿ��Сǿ����������ͼ��ݣ���ͼ�������뿪ͼ��ݵľ���y���ף������ʱ��x���֣�֮��ĺ���ͼ����ͼ����Ϣ������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
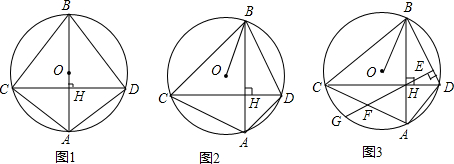
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12 | B�� | 15 | C�� | 12��15 | D�� | 18 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
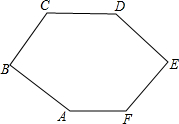 ��ͼ��CD��AF����CDE=��BAF��AB��BC����C=128�㣬��E=80�㣬���F�Ķ�����
��ͼ��CD��AF����CDE=��BAF��AB��BC����C=128�㣬��E=80�㣬���F�Ķ������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com