
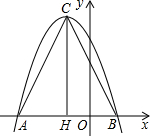
 已知抛物线y=-x2-2x+3交x轴于A、B两点,顶点为C,CH⊥AB交x轴于H,在CH右侧的抛物线上有一点P,已知PQ⊥AC,当∠ACH=∠CPQ时,此时CP的长为( )
已知抛物线y=-x2-2x+3交x轴于A、B两点,顶点为C,CH⊥AB交x轴于H,在CH右侧的抛物线上有一点P,已知PQ⊥AC,当∠ACH=∠CPQ时,此时CP的长为( )| A. | $\frac{4\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{16}{9}$ | D. | $\frac{20}{9}$ |
分析 根据已知条件可以判定△ACH∽△CPQ,首先求出直线CM的解析式为y=2x+6,再联立两函数解析式即可得出交点坐标,根据两点间的距离公式来求CP的长度即可.
解答 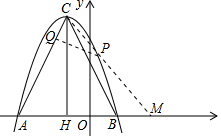 解:∵y=-x2-2x+3=-(x+3)(x-1),或y=-(x+1)2+4,
解:∵y=-x2-2x+3=-(x+3)(x-1),或y=-(x+1)2+4,
∴A(-3,0),B(1,0),C(-1,4),H(-1,0).
∴AC=2$\sqrt{5}$,CH=4,AH=2.
如图,延长CP交X轴于点M.
∵∠ACH=∠CPQ,∠AHC=∠CQP=90°,
∴△ACH∽△CPQ,
∴∠CAH=∠PCQ,
∴AM=CM.
∴AM2=CM2.
设M(m,0),则(m+3)2=42+(m+1)2,
∴m=2,即M(2,0).
设直线CM的解析式为y=kx+b(k≠0).
则 $\left\{\begin{array}{l}{-k+b=4}\\{2k+b=0}\end{array}\right.$,
解之得$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=\frac{8}{3}}\end{array}\right.$,
∴直线CM的解析式y=-$\frac{4}{3}$x+$\frac{8}{3}$.联立 $\left\{\begin{array}{l}{y=-\frac{4}{3}x+\frac{8}{3}}\\{y=-{x}^{2}-2x+3}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{20}{9}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$(舍去).
∴P($\frac{1}{3}$,$\frac{20}{9}$).
∴CP=$\sqrt{(-1-\frac{1}{3})^{2}+(4-\frac{20}{9})^{2}}$=$\frac{20}{9}$.
故选:D.
点评 本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,待定系数法求一次函数解析式,相似三角形的判定与性质,联立两函数解析式求交点坐标,难点在于作辅助线构造出相似三角形并求出直线CP上的一个点的坐标.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
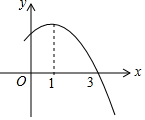 如图是函数y=ax2+bx+c图象的一部分,图象与x轴正半轴交于点(3,0),
如图是函数y=ax2+bx+c图象的一部分,图象与x轴正半轴交于点(3,0),| A. | ① | B. | ②④ | C. | ①②③④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com