Question

已知抛物线y=x²+bx+c，经过点A（0，5）和点B（3，2）
（1）求抛物线的解析式：
（2）现有一半径为l，圆心P在抛物线上运动的动圆，问⊙P在运动过程中，是否存在⊙P与坐标轴相切的情况？若存在，请求出圆心P的坐标；若不存在，请说明理由；
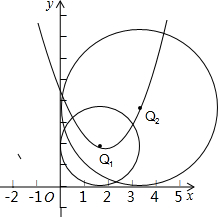
（3）若⊙Q的半径为r，点Q在抛物线上，且⊙Q与两坐轴都相切时，求半径r的值．

Answer 1

分析：（1）利用待定系数法把已知坐标代入抛物线解析式即可
（2）设点P坐标为（x₀，y₀），当⊙P在运动过程中，存在⊙P与坐标轴相切的情况（⊙P与y轴相切；⊙P与x轴相切时）
（3）设点Q坐标为（x，y），则当⊙Q与两条坐标轴都相切时，有y=±x代入抛物线解析式求出x的值即可．

解答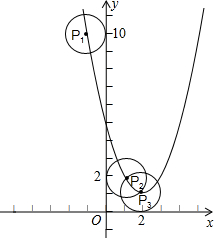：解：（1）由题意，得；

c=5 3b+c+9=2

解得

b=-4 c=5

（3分）
抛物线的解析式为y=x²-4x+5（1分）

（2）当⊙P在运动过程中，存在⊙P与坐标轴相切的情况．
设点P坐标为（x₀，y₀），则
当⊙P与y轴相切时，有|x₀|=1，x₀=±1
由x₀=-1，得y₀=1-4×（-1）+5=10，
∴P₁（-1，10），（1分）
由x₀=1，得y₀=1 ²-4×1+5=2，
∴P₂（1，2）（1分）
当⊙P与x轴相切时有|y₀|=1
∵抛物线开口向上，且顶点在x轴的上方．
∴y₀=1
由y₀=1，得x₀²-4x₀+5=1，
解得x₀=2，
则P₃的坐标是（2，1）
综上所述，符合要求的圆心P有三个，其坐标分别为：
P₁（-1，10），P₂（1，2），P₃（2，1）（2分）

（3）设点Q坐标为（x，y），则当⊙Q与两条坐标轴都相切时，有y=±x
由y=x得x²-4x+5=x，即x²-5x+5=0，
解得x=

5± 5

2

（2分）
由y=-x，得x²-4x+5=-x．
即x²-3x+5=0，此方程无解（1分）
∴⊙O的半径为r=

5± 5

2

．（1分）

点评：本题综合考查的是直线与圆的知识以及二次函数的相关知识点，难度较大．