【题目】若将点A（1，3）向左平移2个单位，再向下平移4个单位得到点B，则点B的坐标为（ ）
A.（﹣2，﹣1）
B.（﹣1，0）
C.（﹣1，﹣1）
D.（﹣2，0）
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线
图象经过A（﹣1，0），B（4，0）两点．
（1）求抛物线的解析式；
（2）若C（m，m﹣1）是抛物线上位于第一象限内的点，D是线段AB上的一个动点（不与端点A、B重合），过点D分别作DE∥BC交AC于E，DF∥AC交BC于F．
①求证：四边形DECF是矩形；
②试探究：在点D运动过程中，DE、DF、CF的长度之和是否发生变化？若不变，求出它的值；若变化，试说明变化情况．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，∠E=∠F=90°，∠B=∠C，AE=AF．给出下列结论：①∠1=∠2；②BE=CF；
③△ACN≌△ABM；④CD=DN．其中正确的是（将正确的结论的序号都填上）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题探究：（1）如图①，AB为⊙O的弦，点C是⊙O上的一点，在直线AB上方找一个点D，使得∠ADB=∠ACB，画出∠ADB；
（2）如图②，AB 是⊙O的弦，点C是⊙O上的一个点，在过点C的直线l上找一点P，使得∠APB<∠ACB，画出∠APB；
（3）如图③，已知足球门宽AB约为
米，一球员从距B点
米的C点（点A、B、C均在球场的底线上），沿与AC成45°的CD方向带球．试问，该球员能否在射线CD上找一点P，使得点P最佳射门点（即∠APB最大）？若能找到，求出这时点P与点C的距离；若找不到，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
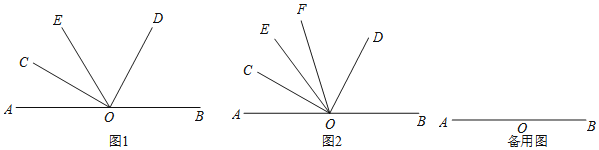
【题目】点O为直线AB上一点，在直线AB上侧任作一个∠COD，使得∠COD=90°．
（1）如图1，过点O作射线OE，当OE恰好为∠AOD的角平分线时，请直接写出∠BOD与∠COE之间的倍数关系，即∠BOD= ______ ∠COE（填一个数字）；
（2）如图2，过点O作射线OE，当OC恰好为∠AOE的角平分线时，另作射线OF，使得OF平分∠COD，求∠FOB+∠EOC的度数；
（3）在（2）的条件下，若∠EOC=3∠EOF，求∠AOE的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AB=5，BC=7，点E是AD上一个动点，把△BAE沿BE向矩形内部折叠，当点A的对应点A1恰好落在∠BCD 的平分线上时，CA1的长为（ ）
A、3或4
B、4或3 C、3或4 D、3或4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
