
【题目】某校为了丰富学生课余生活,计划开设以下课外活动项目:A—版画,B—机器人,C—航模,D—园艺种植.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查(每位学生必须选且只能选一个项目),并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
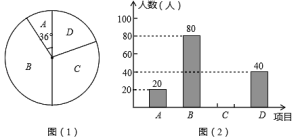
(1)这次被调查的学生共有 人;扇形统计图中,选“D—园艺种植”的学生人数所占圆心角的度数是 °
(2)请你将条形统计图补充完整;
(3)若该校学生总数为1000人,试估计该校学生中最喜欢“机器人”和最喜欢“航模”项目的总人数.
【答案】(1)200、72;(2)见解析;(3)700
【解析】
(1)由A类有20人,所占扇形的圆心角为36°,即可求得这次被调查的学生数,再用360°乘以D人数占总人数的比例可得;
(2)首先求得C项目对应人数,即可补全统计图;
(3)总人数乘以样本中B、C人数所占比例可得.
(1)∵A类有20人,所占扇形的圆心角为36°,
∴这次被调查的学生共有:![]() (人);
(人);
选“D—园艺种植”的学生人数所占圆心角的度数是360°×![]() =72°,
=72°,
故答案为:200、72;
(2)C项目对应人数为:200208040=60(人),补充如图:

(3)1000×![]() =700(人),
=700(人),
答:估计该校学生中最喜欢“机器人”和最喜欢“航模”项目的总人数为700人.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:
【题目】现有三张分别标有数字![]() 、
、![]() 、
、![]() 的卡片,它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为
的卡片,它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为![]() (不放回),再从中任意抽取一张,将上面的数字记为
(不放回),再从中任意抽取一张,将上面的数字记为![]() ,这样的数字
,这样的数字![]() ,
,![]() 能使关于
能使关于![]() 的一元二次方程
的一元二次方程![]() 有两个正根的概率为________.
有两个正根的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
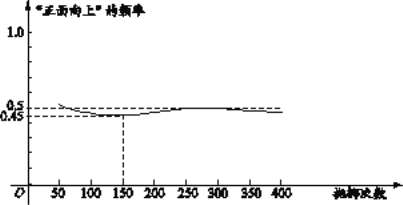
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有![]() 、
、![]() 两个不透明的盒子,
两个不透明的盒子,![]() 盒中装有红色、黄色、蓝色卡片各1张,
盒中装有红色、黄色、蓝色卡片各1张,![]() 盒中装有红色、黄色卡片各1张,这些卡片除颜色外都相同.现分别从
盒中装有红色、黄色卡片各1张,这些卡片除颜色外都相同.现分别从![]() 、
、![]() 两个盒子中任意摸出一张卡片.
两个盒子中任意摸出一张卡片.
(1)从![]() 盒中摸出红色卡片的概率为______;
盒中摸出红色卡片的概率为______;
(2)用画树状图或列表的方法,求摸出的两张卡片中至少有一张红色卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
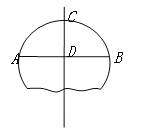
【题目】如图,破残的圆形轮片上,弦AB的垂直平分线交AB于C,交弦AB于D.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)若AB=24cm,CD=8cm,求(1)中所作圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.

(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究![]() ,
,![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐至县城有两座远近闻名的南北古塔,清朝道光11年至13年(公元1831--1833年)修建,南塔名为“文运塔”,高30米;北塔名为“凌云塔”.为了测量北塔的高度AB,身高为1.65米的小明在C处用测角仪CD,(如图所示)测得塔顶A的仰角为45°,此时小明在太阳光线下的影长为1.1米,测角仪的影长为1米.随后,他再向北塔方向前进14米到达H处,又测得北塔的顶端A的仰角为60°,求北塔AB的高度.(参考数据![]() ≈1.414,
≈1.414,![]() ≈1.732,结果保留整数)
≈1.732,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
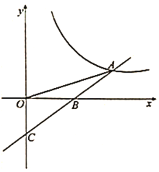
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图1,平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() .双曲线
.双曲线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
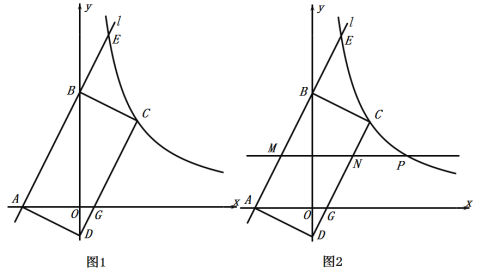
(1)求![]() 的值;
的值;
(2)在图1中以线段![]() 为边作矩形
为边作矩形![]() ,使顶点
,使顶点![]() 在第一象限、顶点
在第一象限、顶点![]() 在
在![]() 轴负半轴上.线段
轴负半轴上.线段![]() 交
交![]() 轴于点
轴于点![]() .直接写出点
.直接写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)如图2,在(2)题的条件下,已知点![]() 是双曲线
是双曲线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的平行线分别交线段
轴的平行线分别交线段![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
请从下列![]() ,
,![]() 两组题中任选一组题作答.我选择组题.
两组题中任选一组题作答.我选择组题.
A.①当四边形![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②在①的条件下,连接![]() ,
,![]() .坐标平面内是否存在点
.坐标平面内是否存在点![]() (不与点
(不与点![]() 重合),使以
重合),使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,直接写出点
全等?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
B.①当四边形![]() 成为菱形时,求点
成为菱形时,求点![]() 的坐标;
的坐标;
②在①的条件下,连接![]() ,
,![]() .坐标平面内是否存在点
.坐标平面内是否存在点![]() (不与点
(不与点![]() 重合),使以
重合),使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,直接写出点
全等?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com