
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC=4![]() .一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止,在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(t>0)
.一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止,在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(t>0)
(1)在整个运动过程中,判断PE与AB的位置关系是
(2)如图2,当点D在线段AB上时,连接AQ、AP,是否存在这样的b,使得AP=PQ?若存在,求出对应的t的值;若不存在,请说明理由;
(3)当t=4时,点D经过点A:当t=![]() 时,点E在边AB上.设△ABC与△PQE重叠部分的面积为S,请求出在整个运动过程中S与t之间的函数关系式,以及写出相应的自变量t的取值范围,并求出当4<t≤
时,点E在边AB上.设△ABC与△PQE重叠部分的面积为S,请求出在整个运动过程中S与t之间的函数关系式,以及写出相应的自变量t的取值范围,并求出当4<t≤![]() 时S的最大值.
时S的最大值.
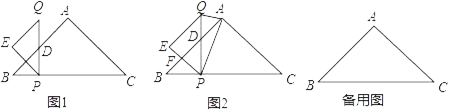
【答案】(1)PE与AB互相垂直,理由详见解析;(2)t的值为![]() ;(3)详见解析.
;(3)详见解析.
【解析】
(1)结论:PE与AB互相垂直.理由等腰直角三角形的性质即可证明.
(2)如图2中,过点A作AH⊥BC于点H.根据AP=PQ,构建方程即可解决问题.
(3)分三种情形:①如图3﹣1中,当0<t≤4时.△ABC与△PQE的重叠部分为△PFD.②如图3﹣2中,当4<t≤![]() 时,△ABC与△PQE的重叠部分为四边形PDAF.③如图3﹣3中,当
时,△ABC与△PQE的重叠部分为四边形PDAF.③如图3﹣3中,当![]() <t≤8时,△ABC与△PQE的重叠部分为四边形FEPD.分别求解即可.
<t≤8时,△ABC与△PQE的重叠部分为四边形FEPD.分别求解即可.
解:(1)结论:PE与AB互相垂直.
理由:如图1中,设PE交AB于K.
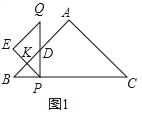
∵△ABC,△PQE都是等腰直角三角形,
∴∠B=∠EPQ=45°,
∵PQ⊥BC,
∴∠BPQ=90°,
∴∠EPB=90°,
∴∠B+∠EPB=90°,
∴∠PKB=90°,
∴PE⊥AB.
(2)如图2中,过点A作AH⊥BC于点H.
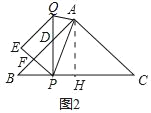
∵Rt△ABC中,AB=AC=4![]()
∴BC=![]() =8,
=8,
∴AH=BH=CH=4,
依题意得BP=t.PH=BH﹣BP=4﹣t,
∴PA=![]() =
=![]() ,
,
∵PD⊥BC,∠B=45°,
∴PD=BP=t,PQ=2PD=2t,
∵PQ=AP,
∴2t=![]() ,
,
解得:t=![]() 或
或![]() (舍弃),
(舍弃),
∴t的值为![]() .
.
(3)如图3﹣1中,△ABC与△PQE的重叠部分为△PFD.
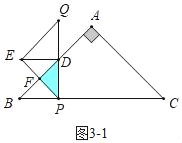
由题意可得△PFD、△BPD为等腰直角三角形,
∴BP=PD=t,
∴PF=DF=PDcos45°=![]() t,
t,
∴S=![]() PFDF=
PFDF=![]() (0<t≤4).
(0<t≤4).
如图3﹣2中,△ABC与△PQE的重叠部分为四边形PDAF.

由题意可得△PFB、△PDC为等腰直角三角形,
∵BP=t,PC=BC﹣PB=8﹣t,
∴BF=PF=![]() t,DP=PC=8﹣t,
t,DP=PC=8﹣t,
∴S=S△ABC﹣S△PFB﹣S△PDC
=![]() ×4
×4![]() ×4
×4![]() ﹣
﹣![]() ×
×![]() t×
t×![]() t﹣
t﹣![]() (8﹣t)(8﹣t)
(8﹣t)(8﹣t)
=﹣![]() t2+8t﹣16(4<t≤
t2+8t﹣16(4<t≤![]() )
)
=﹣(![]() t﹣
t﹣![]() )2+
)2+![]()
∵﹣![]() <0,
<0,
∴当x=![]() 时,S有最大值
时,S有最大值![]() .
.
如图3﹣3中,△ABC与△PQE的重叠部分为四边形FEPD.

∵CP=PD=8﹣t,
∴QD=PD=8﹣t,PQ=16﹣2t,
由题意可得△QDF为等腰直角三角形
∴QF=![]() (8﹣t),QE=
(8﹣t),QE=![]() (16﹣2t),
(16﹣2t),
∴S=S△PQE﹣S△QDF
=![]() ×
×![]() (16﹣2t)
(16﹣2t)![]() (16﹣2t)﹣
(16﹣2t)﹣![]() ×
×![]() (8﹣t)×
(8﹣t)×![]() (8﹣t)
(8﹣t)
=![]()
![]() ﹣12t+48(
﹣12t+48(![]() <t≤8).
<t≤8).


科目:初中数学 来源: 题型:
【题目】如图1,平面内有一点P到△ABC的三个顶点的距离分别为PA、PB、PC,若有PA2=PB2+PC2则称点P为△ABC关于点A的勾股点.
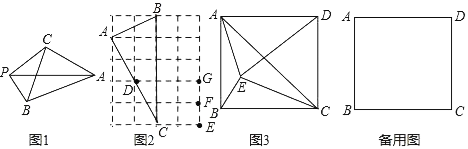
(1)如图2,在4×5的网格中,每个小正方形的长均为1,点A、B、C、D、E、F、G均在小正方形的顶点上,则点D是△ABC关于点 的勾股点;在点E、F、G三点中只有点 是△ABC关于点A的勾股点.
(2)如图3,E是矩形ABCD内一点,且点C是△ABE关于点A的勾股点,
①求证:CE=CD;②若DA=DE,∠AEC=120°,求∠ADE的度数.
(3)矩形ABCD中,AB=5,BC=6,E是矩形ABCD内一点,且点C是△ABE关于点A的勾股点,
①若△ADE是等腰三角形,求AE的长;②直接写出AE+![]() BE的最小值.
BE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
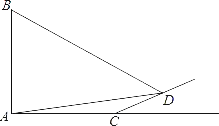
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:![]() ,求旗杆AB的高度(
,求旗杆AB的高度(![]() ,结果精确到个位).
,结果精确到个位).
查看答案和解析>>
科目:初中数学 来源: 题型:
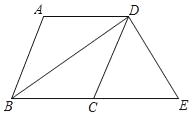
【题目】如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组的同学测量一架无人飞机P的高度,如图,A,B两个观测点相距![]() ,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:
,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:![]() ,
,![]() ,sin71°≈0.95,tan71°≈2.90)
,sin71°≈0.95,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
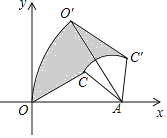
【题目】如图,△OAC的顶点O在坐标原点,OA边在x轴上,OA=2,AC=1,把△OAC绕点A按顺时针方向旋转到△O′AC′,使得点O′的坐标是(1,![]() ),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
),则在旋转过程中线段OC扫过部分(阴影部分)的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是直径,过点O作OD⊥CB,垂足为点D,延长DO交⊙O于点E,过点E作PE⊥AB,垂足为点P,作射线DP交CA的延长线于F点,连接EF,
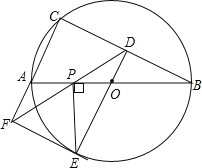
(1)求证:OD=OP;(2)求证:FE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
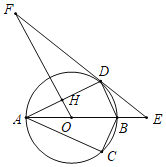
【题目】如图,在Rt△ABC中,∠ACB=90°,点O为△ABC外接圆的圆心,将△ABC沿AB翻折后得到△ABD.
(1)求证:点D在⊙O上;
(2)在直径AB的延长线上取一点E,使DE2=BEAE.
①求证:直线DE为⊙O的切线;
②过点O作OF∥BD交AD于点H,交ED的延长线于点F.若⊙O的半径为5,cos∠DBA=![]() ,求FH的长.
,求FH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com