

分析 (1)根据图案①、②、③中火柴棒的数量可知,第1个图形中火柴棒有8根,每多一个多边形就多7根火柴棒,由此可知第n个图案需火柴棒8+7(n-1)=7n+1根,令n=7可得答案.
(2)令8+7(n-1)=7n+1=2017求得n值即可.
解答 解:(1)∵图案①需火柴棒:8根;
图案②需火柴棒:8+7=15根;
图案③需火柴棒:8+7+7=22根;
…
∴图案n需火柴棒:8+7(n-1)=7n+1根;
当n=7时,7n+1=7×7+1=50,
∴图案⑦需50根火柴棒;
故答案为:50.
(2)令7n+1=2017,
解得n=288,
故2017是第288个图案.
点评 此题主要考查了图形的变化类,解决此类题目的关键在于图形在变化过程中准确抓住不变的部分和变化的部分,变化部分是以何种规律变化.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
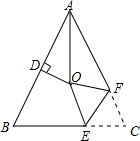 如图,△ABC中,AB=AC,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合.若∠OEC=136°,则∠BAC的大小为( )
如图,△ABC中,AB=AC,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合.若∠OEC=136°,则∠BAC的大小为( )| A. | 44° | B. | 58° | C. | 64° | D. | 68° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
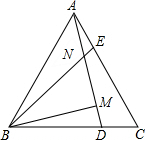 已知:△ABC为等边三角形,点D、E分别在BC和AC上,并且CD=AE,连接AD、BE相交于点N,过点B作BM⊥AD于点M.
已知:△ABC为等边三角形,点D、E分别在BC和AC上,并且CD=AE,连接AD、BE相交于点N,过点B作BM⊥AD于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com