
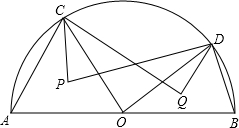
 如图已知AB为半⊙O的直径,C、D为弧$\widehat{AB}$上两点,P、Q分别为△OAC、△OBD的外心.证明:CP•CQ=DP•DQ.
如图已知AB为半⊙O的直径,C、D为弧$\widehat{AB}$上两点,P、Q分别为△OAC、△OBD的外心.证明:CP•CQ=DP•DQ. 分析 连接AP,OP,AD,BQ,OQ,BC,只要证明△APD∽△QBC,即可解决问题.
解答 解:连接AP,OP,AD,BQ,OQ,BC,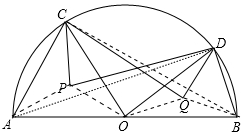
设∠BAD=α,∠ABC=β,
∵∠OAP=∠AOP=$\frac{1}{2}∠$AOC=∠ABC=β,∠OBQ=∠BOQ=$\frac{1}{2}∠$BOD=∠BAD=α,
∴∠PAD=∠OAP-∠OAD=β-α=∠OBC-∠OBQ=∠QBC,
∵$\frac{AD}{AP}=\frac{AD}{AB}•\frac{AB}{AO}•\frac{AO}{AP}$=cosα×2×2cosβ=4cosα×cosβ,
同理$\frac{BC}{BQ}$=4cosα×cosβ,
∴$\frac{AD}{AP}$=$\frac{BC}{BQ}$,
∴$\frac{AD}{BC}$=$\frac{AP}{BQ}$∵∠PAD=∠QBC,
∴△APD∽△QBC,
∴$\frac{AP}{QB}$=$\frac{PD}{CQ}$,∵PA=PC,BQ=DQ,
∴$\frac{PC}{DQ}$=$\frac{PD}{CQ}$,
∴CP•CQ=DP•DQ.
点评 本题考查相似三角形的判定和性质、三角形的外心与外接圆等知识,解题的关键是学会添加辅助线,构造相似三角形,题目比较难,属于竞赛题目.


科目:初中数学 来源: 题型:填空题
 如图,已知点A(1,2),B(2,1),若点P是x轴上动点,点Q是y轴上动点,点P满足|PA-PB|的值最大,点Q满足QA+QB的值最小,则PQ=$\frac{\sqrt{106}}{3}$.
如图,已知点A(1,2),B(2,1),若点P是x轴上动点,点Q是y轴上动点,点P满足|PA-PB|的值最大,点Q满足QA+QB的值最小,则PQ=$\frac{\sqrt{106}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
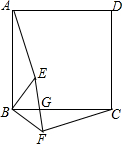 如图,在正方形ABCD中,BE⊥BF,BE=BF,EF交BC于点G.
如图,在正方形ABCD中,BE⊥BF,BE=BF,EF交BC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com