解:(1)答案为:-

,

;
(2)①根据题意得x
1+x
2=4,x
1•x
2=2,
所以(x
1-1)(x
2-1)=x
1•x
2-(x
1+x
2)+1=2-4+1=-1;
②∵a是方程x
2+2x-2013=0的根,
∴a
2+2a-2013=0,即a
2=-2a+2013,
∴a
2+3a+b=-2a+2013+3a+b
=a+b+2013,
∵a、b是方程x
2+2x-2013=0的两个实数根,
∴a+b=-2,
∴a
2+3a+b=-2+2013=2011.
分析:(1)根据根与系数的关系填空;
(2)①先根据根与系数的关系得到x
1+x
2=4,x
1•x
2=2,再把(x
1-1)(x
2-1)展开,变形得到x
1•x
2-(x
1+x
2)+1,然后利用整体代入的方法计算;
②先根据方程的根的定义得到a
2+2a-2013=0,即a
2=-2a+2013,则原式=a+b+2013,然后根据根与系数的关系得到a+b=-2,再利用整体代入的方法计算.
点评:本题考查了一元二次方程ax
2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x
1,x
2,则x
1+x
2=-

,x
1•x
2=

.也考查了一元二次方程的解.

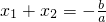 ,
,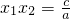 .这一结论称为一元二次方程根与系数关系,它的应用很多,请完成下列各题:
.这一结论称为一元二次方程根与系数关系,它的应用很多,请完成下列各题: ,
, ;
; ,x1•x2=
,x1•x2= .也考查了一元二次方程的解.
.也考查了一元二次方程的解. 

 同步练习强化拓展系列答案
同步练习强化拓展系列答案