
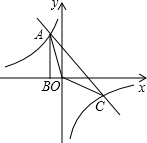
 如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与y=-x-(k+1)在第二象限的交点,AB⊥x轴于B且S△ABO=$\frac{3}{2}$.
如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与y=-x-(k+1)在第二象限的交点,AB⊥x轴于B且S△ABO=$\frac{3}{2}$.分析 (1)根据反比例函数系数k的几何意义可知$\frac{1}{2}$|k|=$\frac{3}{2}$,由此得出k=±3,再结合反比例函数图象在第二、四象限,即可得出k=-3,将k=-3代入两函数解析式即可得出结论;
(2)联立两函数解析式成方程组,解方程组求出交点A、C的坐标,结合函数图象的上下位置关系即可解出不等式的解集.
解答 解:(1)∵AB⊥x轴于B且S△ABO=$\frac{1}{2}$|k|=$\frac{3}{2}$,
∴k=±3.
又∵反比例函数的图象在第二、四象限,
∴k=-3,
∴反比例函数的解析式为y=-$\frac{3}{x}$,一次函数的解析式为y=-x-(-3+1)=-x+2.
(2)联立反比例函数与一次函数解析式,
$\left\{\begin{array}{l}{y=-\frac{3}{x}}\\{y=-x+2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=3}\\{{y}_{2}=-1}\end{array}\right.$.
∴点A的坐标为(-1,3),点C的坐标为(3,-1).
观察两函数图象,发现:
当-1<x<0或x>3时,一次函数的图象在反比例函数图象的下方,
∴一次函数的值小于反比例函数的值的x的取值范围为-1<x<0或x>3.
点评 本题考查了反比例函数与一次函数的交点的问题、反比例函数系数k的几何意义已经解二元一次方程组,解题的关键是:(1)求出k值;(2)求出交点A、C的坐标.本题属于基础题,难度不大,解集该题型题目时,由三角形的面积结合反比例系数k的几何意义以及函数图象求出反比例函数系数k的值时关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
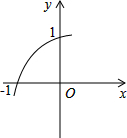 已知函数y=ax2+bx+c的图象的一部分如图所示.该图象过点(-1,0)和(0,1),且顶点在笫一象限,则a+b+c的取值范围是0<a+b+c<2.
已知函数y=ax2+bx+c的图象的一部分如图所示.该图象过点(-1,0)和(0,1),且顶点在笫一象限,则a+b+c的取值范围是0<a+b+c<2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
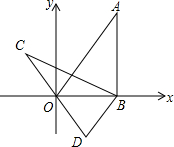 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )| A. | (-2,2$\sqrt{3}$) | B. | (-4,2$\sqrt{3}$) | C. | (-2$\sqrt{3}$,2) | D. | (-2$\sqrt{3}$,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
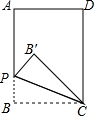 如图,在矩形ABCD中,AB=4,BC=3,点P是AB上(不含端点A,B)任意一点,把△PBC沿PC折叠,当点B′的对应点落在矩形ABCD的对角线上时,BP=$\frac{3}{2}$或$\frac{9}{4}$.
如图,在矩形ABCD中,AB=4,BC=3,点P是AB上(不含端点A,B)任意一点,把△PBC沿PC折叠,当点B′的对应点落在矩形ABCD的对角线上时,BP=$\frac{3}{2}$或$\frac{9}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com