

���� ��1�������ABC���ߵĸ�Ϊ4$\sqrt{3}$sin60��=4$\sqrt{3}$��$\frac{\sqrt{3}}{2}$=6������A���D�غ�ʱ����EF���������˶���2$\sqrt{3}$�����ɵó������
��2��������������������ε������ʽ���Ա�ʾ��0��t��2$\sqrt{3}$ʱ�ص����ֵ��������2$\sqrt{3}$��t��6ʱ��S��ABC-$\frac{��4\sqrt{3}-t����4\sqrt{3}-t��\sqrt{3}}{2}$�Ϳ�������ص����ֵ������
��3������A���D�غ�ʱ��BE=CE=2$\sqrt{3}$�����������������AN��ֵ������������������AH��ֵ����AN=AH=4ʱ����AN=NH=4ʱ����ʱH�����߶�AG���ӳ����ϣ���AH=NHʱ����ʱH��Ϊ�߶�AG���д�����AG�Ľ��㣬�Ӷ���������𰸣�
��� �⣺��1���ߡ�ABCΪ�߳���4$\sqrt{3}$�ĵȱ������Σ�
���ABC���ߵĸ�Ϊ4$\sqrt{3}$sin60��=4$\sqrt{3}$��$\frac{\sqrt{3}}{2}$=6��
���ı���DEFG�DZ߳���6�������Σ�
���ABC��ͼ�ٵ�λ�ó�������EF���������˶�ʱ����A���D���غϣ�
����A���D�غ�ʱ����EF���������˶���$\frac{4\sqrt{3}}{2}$=2$\sqrt{3}$��
����ÿ��1����λ���ȵ��ٶ���EF�������������˶���
��t=$\frac{2\sqrt{3}}{1}$=2$\sqrt{3}$���룩��
��2�������������
�ٵ�0��t��2$\sqrt{3}$ʱ��S=$\frac{1}{2}$t•t•tan60��=$\frac{1}{2}$t2��$\sqrt{3}$=$\frac{\sqrt{3}}{2}$t2��
�ڵ�2$\sqrt{3}$��t��6ʱ��S=S��ABC-$\frac{1}{2}$��4$\sqrt{3}$-t����4$\sqrt{3}$-t��tan60��=$\frac{1}{2}$��6��4$\sqrt{3}$-$\frac{1}{2}$��48-8$\sqrt{3}$t+t2��$\sqrt{3}$=-$\frac{\sqrt{3}}{2}$t2+12t-12$\sqrt{3}$��
��3������A���D�غ�ʱ��BE=CE=2$\sqrt{3}$
��BMƽ�֡�ABE��
���MBE=$\frac{1}{2}$��ABE=30�㣬
��ME=BEtan30��=2$\sqrt{3}$��$\frac{\sqrt{3}}{3}$=2��
�ߡ�ABM=��BAM��
��AM=BM=4��
����ת�����ʵã���ABM�ա�ACN��
���CAN=30�㣬AN=4��
��ANHΪ���������η�����������ۣ�
��AN=AH=4ʱ��
��AG=6��
���ANH�������������
��AN=NH=4ʱ��
�ߡ�CAE=30�㡢��CAN=30�㣬
���NAG=30�㣬
��AH=2ANcot30��=2��4��$\sqrt{3}$=8$\sqrt{3}$��6��
��H�����߶�AG���ӳ����ϣ�
���������ȥ��
��AH=NHʱ����H��Ϊ�߶�AN���д�����AG�Ľ��㣬��ͼ��ʾ��
��AK=$\frac{1}{2}$AN=2��AH=$\frac{AK}{cos��HAK}$=$\frac{2}{cos30��}$=$\frac{4}{3}$$\sqrt{3}$��
���� ���⿼���˵ȱ������ε����ʡ������ε����ʡ���ת�����ʡ����������ε��ж������Ǻ�����֪ʶ�������ۺ���ǿ����һ���Ѷȣ�����������ת�����ʡ��ȱ������κ������ε������ǽ������Ĺؼ���


 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д� Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
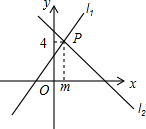 ��ͼl1��y=x+3��l2��y=ax+b�ཻ�ڵ�P��m��4���������x�IJ���ʽx+3��ax+b�Ľ�Ϊ��������
��ͼl1��y=x+3��l2��y=ax+b�ཻ�ڵ�P��m��4���������x�IJ���ʽx+3��ax+b�Ľ�Ϊ��������| A�� | x��4 | B�� | x��m | C�� | x��m | D�� | x��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �װ� | B�� | �Ұ� | C�� | ����һ������ | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m=2��n=3 | B�� | m=2��n=1 | C�� | m=2��n=0 | D�� | m=1��n=2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com