
 如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.
如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.分析 (1)先利用三角形内角和计算出∠B=57°,然后根据平移的性质确定∠E的值;
(2)根据平移的性质得到AB=DE,则AD=BE,然后利用AD+BD+BE=AE得到BE+2+BE=9,再解关于BE的方程即可.
解答 解:(1)∵∠ACB=90°,∠A=33°
∴∠B=90°-33°=57°,
∵三角形ABC沿AB方向向右平移得到三角形DEF,
∴∠E=∠B=57°;
(2)∵三角形ABC沿AB方向向右平移得到三角形DEF,
∴AB=DE,
∴AD=BE,
∴AD+BD+BE=AE,
即BE+2+BE=9,
∴BE=3.5(cm).
点评 本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:解答题
 如图:矩形ABCD中,AB=4,BC=8,将矩形折叠,使点C与点A重合,折痕为EF,点D的对应点为G,连接DG,
如图:矩形ABCD中,AB=4,BC=8,将矩形折叠,使点C与点A重合,折痕为EF,点D的对应点为G,连接DG,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
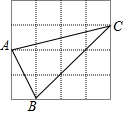 如图,在4×4的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则该三角形最长边的长为( )
如图,在4×4的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则该三角形最长边的长为( )| A. | $\sqrt{5}$ | B. | $\sqrt{17}$ | C. | $3\sqrt{2}$ | D. | $5\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
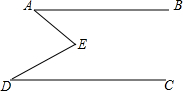 如图,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
如图,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分 组(m) | 频数(名) | 频率 |
| 1.565~1.595 | 2 | 0.04 |
| 1.595~1.625 | 4 | 0.08 |
| 1.6254~1.655 | 6 | 0.12 |
| 1.655~1.685 | 11 | 0.22 |
| 1.685~1.715 | 17 | 0.34 |
| 1.715~1.745 | 6 | 0.12 |
| 1.745~1.775 | 4 | 0.08 |
| 合 计 | 50 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com