

分析 如图,作辅助线;首先运用翻折变换的性质证明AE=CE(设为λ),进而得到DE=8-λ,此为解决问题的关键性结论;其次证明△CDE为直角三角形,运用勾股定理列出关于λ的方程,求出λ即可解决问题.
解答 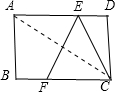 解:如图,连接AC;
解:如图,连接AC;
由翻折变换的性质得:
EF⊥AC,且EF平分AC,
∴AE=CE(设为λ);则DE=8-λ;
∵四边形ABCD为矩形,
∴∠D=90°,CD=AB=6;
由勾股定理得:
CE2=CD2+DE2,
即λ2=(8-λ)2+62,
解得:λ=$\frac{25}{4}$.
故答案为$\frac{25}{4}$.
点评 该题主要考查了翻折变换的性质、矩形的性质、勾股定理等几何知识点及其应用问题;解题的方法是作辅助线,还原图形中隐含的等量关系;解题的关键是灵活运用翻折变换的性质、矩形的性质、勾股定理等几何知识点来分析、判断、推理或解答.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x+y=18 | B. | x+y=36 | C. | 4x+2y=36 | D. | 2x+4y=36 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{37}$ | B. | $\sqrt{13}$ | C. | $\sqrt{37}$、$\sqrt{13}$ | D. | $\sqrt{37}$、$\sqrt{13}$、5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
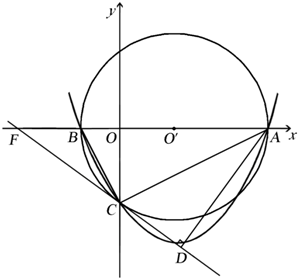 如图,抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4与x轴交于点A和点B(点B在点A的左侧),与轴交于点C,⊙O′是△ABC的外接圆,AB是⊙O′的直径,过点C作⊙O′的切线与x轴交于点F,过点A作AD⊥CF于点D.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4与x轴交于点A和点B(点B在点A的左侧),与轴交于点C,⊙O′是△ABC的外接圆,AB是⊙O′的直径,过点C作⊙O′的切线与x轴交于点F,过点A作AD⊥CF于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),这个容器的形状是下图中的( )
匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),这个容器的形状是下图中的( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com