
【题目】已知等边△ABC的两个顶点坐标为A(-3,0),B(3,0),则点![]() 的坐标为____,△ABC的面积为____.
的坐标为____,△ABC的面积为____.
【答案】(0,![]() )或(0,-
)或(0,-![]() )
) ![]()
【解析】
根据A、B坐标及等边三角形的性质可得点C在y轴上,如图,当点C在y轴正半轴时,由AC1=AB=6,OA=3,利用勾股定理求出OC1的长即可得点C1坐标;同理可求出点C在y轴负半轴时C2的坐标;根据S△ABC=![]() AB·OC即可求出△ABC的面积.
AB·OC即可求出△ABC的面积.
∵A(-3,0),B(3,0),
∴AB中点为(0,0),AB=6,
∵△ABC是等边三角形,
∴点C在y轴上,AC=AB=6,OA=3,
如图,当点C在y轴正半轴时,
OC1=![]() =3
=3![]() ,
,
∴C1(0,3![]() ),
),
当点C在y轴负半轴时,
同理可得:OC2=3![]() ,
,
∴C2(0,-3![]() ),
),
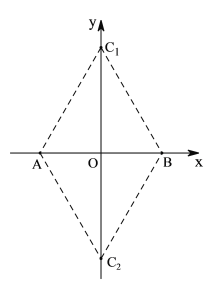
综上所述:点C坐标为(0,3![]() )或(0,-3
)或(0,-3![]() ),
),
∴S△ABC=![]() AB·OC=9
AB·OC=9![]() ,
,
故答案为:(0,3![]() )或(0,-3
)或(0,-3![]() );9
);9![]()


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(﹣3,0),点B是x轴上异于点A一动点,设B(x,0),以AB为边在x轴的上方作正方形ABCD.

(1)如图(1),若点B(1,0),则点D的坐标为 ;
(2)若点E是AB的中点,∠DEF=90°,且EF交正方形外角的平分线BF于F.
①如图(2),当x>0时,求证:DE=EF;
②若点F的纵坐标为y,求y关于x的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BCA=90°,∠A<∠ABC,D是AC边上一点,且DA=DB,O是AB的中点,CE是△BCD的中线.
(1)如图a,连接OC,请直接写出∠OCE和∠OAC的数量关系: ;
(2)点M是射线EC上的一个动点,将射线OM绕点O逆时针旋转得射线ON,使∠MON=∠ADB,ON与射线CA交于点N.
①如图b,猜想并证明线段OM和线段ON之间的数量关系;
②若∠BAC=30°,BC=m,当∠AON=15°时,请直接写出线段ME的长度(用含m的代数式表示).
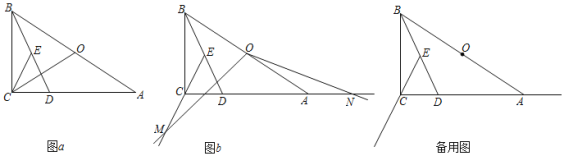
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园的门票每张20元,一次性使用.考虑到人们的不同需求,也为了吸引更多的游客,该公园除保留原来的售票方法外,还推出了一种“购买个人年票”(个人年票从购买日起,可供持票者使用一年)的售票方法.年票分A,B,C三类,A类年票每张240元,持票进入该园区时,无需再购买门票;B类年票每张120元,持票者进入该园区时,需再购买门票,每次4元;C类年票每张80元,持票者进入该园区时,需再购买门票,每次6元.
(1)如果只能选择一种购买年票的方式,并且计划在一年中花费160元在该公园的门票上,通过计算,找出可进入该园区次数最多的方式.
(2)一年中进入该公园超过多少次时,A类年票比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:
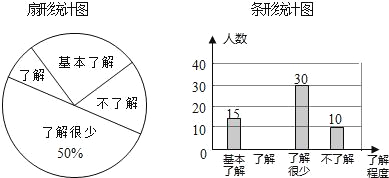
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 度;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )

A. 13B. 14C. 15D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com