一个不透明的布袋内装有形状、大小、质地等完全相同的4个小球,分别标有数字1,2,3,4
(1)从布袋中随机地取出一个小球,则小球上所标的数字恰好为4的概率是______;
(2)从布袋中随机地取出一个小球,记录小球上所标的数字为x,不将取出的小球放回布袋,再随机地取出一个小球,记录小球上所标的数字为y,这样就确定点P的一个坐标为(x,y),求点P落在直线y=x+1上的概率;
(3)从布袋中随机地取出一个小球,用小球上所标的数字作为十位上的数字,将取出的小球放回布袋后,再随机地取出一个小球,用小球上所标的数字作为个位上的数字,求组成的两位数恰好是3的倍数的概率.
解:(1)根据题意可得:共4个小球,标有1,2,3,4故从布袋中随机地取出一个小球,则小球上所标的数字恰好为4的概率是

;
(2)满足条件的点有:(1,2)、(1,3)、(1,4)、(2,1)、(2,3)、(2,4)、(3,1)、(3,2)、(3,4)、(4,1)、(4,2)、(4,3)共12个,
其中落在直线y=x+1的有(1,2)、(2,3)、(3,4)三点,所以p=
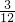
=

;
(3)所有的两位数有:11,12,13,14,21,22,23,24,31,32,33,34,41,42,43,44共16个,
其中是3的倍数的是:12,21,24,33,42五个,所以p=
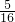
.
分析:根据随机事件概率大小的求法,找准两点:
①符合条件的情况数目;
②全部情况的总数.
二者的比值就是其发生的概率的大小.
点评:本题考查随机事件率的求法与运用,一般方法为:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
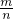
.

 ;
;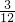 =
= ;
;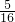 .
.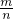 .
. 

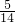 ,则可以向布袋内加入________.
,则可以向布袋内加入________.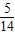 ,则可以向布袋内加入 .
,则可以向布袋内加入 . ,则可以向布袋内加入( )。
,则可以向布袋内加入( )。