
分析 (1)设甲货仓原来库存的电脑有a台,则乙货仓原来库存的电脑有(500-a)台,根据“从甲货仓调运95台电脑到乙货仓,这时乙货仓的电脑数比甲货仓的电脑数的两倍还多50台”建立方程,解方程即可;
(2)设从甲货仓调运到A电脑城的电脑为x台,则从乙货仓调到B电脑城的电脑数为350-(300-x)=50+x;
(3)设总调运费用为y元,根据题意得出y=12x+10(150-x)+18(300-x)+14(50+x),得y=-2x+7600,再求出自变量的取值范围,然后根据一次函数的性质即可求解.
解答 解:(1)设甲货仓原来库存的电脑有a台,则乙货仓原来库存的电脑有(500-a)台,根据题意得
500-a+95=2(a-95)+50,
解得a=245,
500-a=255,a-95=150,500-a+95=350.
答:甲、乙两个货仓原来库存的电脑各有245台、255台;甲、乙两个货仓现在库存的电脑各有150台、350台;
(2)350-(300-x)=50+x;
(3)设总调运费用为y元
y=12x+10(150-x)+18(300-x)+14(50+x),
化简,得y=-2x+7600,
由x≥0且150-x≥0且300-x≥0,
得0≤x≤150.
∵k<0时,
∴x取最大时,y最小,
∴x取150时,y有最小值7300.
答:甲货仓分别运到 A、B 两个电脑城150台、0台,乙货仓分别运到 A、B 两个电脑城150台、200台;最低的总调运费用为7300元.
点评 本题考查的是一次函数的应用,一元一次方程的应用,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.


科目:初中数学 来源: 题型:选择题
| A. | (2x-y)2=4x2-2xy+y2 | B. | (a-b)2=(b-a)2 | ||
| C. | ($\frac{1}{2}$a-b)2=$\frac{1}{4}$a2+ab+b2 | D. | (x+2y)2=x2+4y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
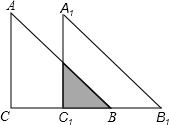 如图,Rt△ABC中∠C=90°,AC=BC=4,将△ABC沿CB方向移动到△A1B1C1的位置,
如图,Rt△ABC中∠C=90°,AC=BC=4,将△ABC沿CB方向移动到△A1B1C1的位置,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com