
【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
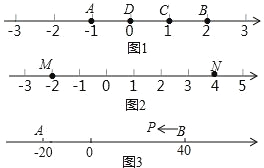
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
【答案】(1)点D是(B,C)的奇异点,不是(A,B)的奇异点;(2)(M,N)的奇异点表示的数是2;(3)①点P表示的数是0或10或20时,P、A、B中恰有一个点为其余两点的奇异点;②PB=120或180或90.
【解析】
(1)根据奇异点的定义和数轴上两点间的距离,即可求出点D到点A的距离为1,到点B的距离为2,以及点D到点C的距离为1,就可以对点D做出判断.
(2)设奇异点表示的数为x,根据奇异点的定义可得方程:x﹣(﹣2)=2(4﹣x).从而求得x值.
(3)①当P在A、B两点之间时,P、A、B中恰有一个点为其余两点的奇异点需分类讨论,具体分四种情况讨论:当点P是(A,B)的奇异点时、当点P是(B,A)的奇异点时、当点A是(B,P)的奇异点时、当点B是(A,P)的奇异点时,计算方法同(1).
②点P到达点A后继续向左运动,是否存在使得P、A、B中恰有一个点为其余两点的奇异点的情况方法同①分四种情况讨论:当点P为(B,A)的奇异点时,PB=120;
当点A为(P,B)的奇异点时,PB=180;当点A为(B,P)的奇异点时,PB=90;
当点B为(P,A)的奇异点时,PB=120.
(1)在图1中,点D到点A的距离为1,到点B的距离为2,
∴点D是(B,C)的奇异点,不是(A,B)的奇异点;
(2)设奇异点表示的数为x,
则由题意,得x﹣(﹣2)=2(4﹣x).
解得x=2.
∴(M,N)的奇异点表示的数是2;
(3)①设点P表示的数为y.
当点P是(A,B)的奇异点时,
则有y+20=2(40﹣y),
解得y=20.
当点P是(B,A)的奇异点时,
则有40﹣y=2(y+20),
解得y=0.
当点A是(B,P)的奇异点时,
则有40+20=2(y+20),
解得y=10.
当点B是(A,P)的奇异点时,
则有40+20=2(40﹣y),解得y=10.
∴当点P表示的数是0或10或20时,
P、A、B中恰有一个点为其余两点的奇异点.
②当点P为(B,A)的奇异点时,PB=120;
当点A为(P,B)的奇异点时,PB=180;
当点A为(B,P)的奇异点时,PB=90;
当点B为(P,A)的奇异点时,PB=120.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
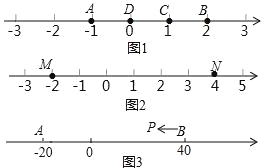
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于点M,交DC于点N,设AE=x,BM=y,则y与x的大致图象是( )

A. B.
B. C.
C. D.
D.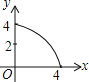
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”国庆期间出租车司机小李某天下午的营运始终在长安街(自东向西或自西向东)上进行,如果规定向东为正,向西为负,他这天下午从天安门出发,行车里程(单位:千米)如下:
+15,﹣2,+5,﹣1,+10,﹣3,﹣2,+12,+4,﹣5,+6.
(1)小李将最后一名乘客送抵目的地时,小李距天安门有多远?
(2)如果汽车耗油量为0.08升/千米,这天下午小李共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在9×9网格中,每个小方格的边长看作单位1,每个小方格的顶点叫作格点,△ABC的顶点都在格点上.
(1)请在网格中画出△ABC的一个位似图形△A1B1C,使两个图形以点C为位似中心,且所画图形与△ABC的相似比为2∶1;
(2)将△A1B1C绕着点C顺时针旋转90°得△A2B2C,画出图形,并在如图所示的坐标系中分别写出△A2B2C三个顶点的坐标.
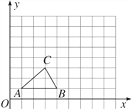
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D,依此类推,则旋转第2016次后,得到的等腰直角三角形的直角顶点P2017的坐标为( )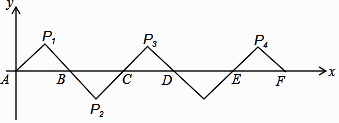
A.(4030,1)
B.(4029,﹣1)
C.(4033,1)
D.(4031,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2017次后,顶点A在整个旋转过程中所经过的路程之和为 . 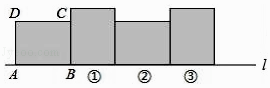
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com