
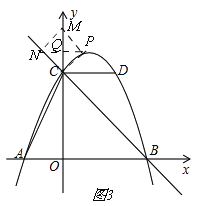
【题目】如图,抛物线![]() 的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC,CD.
的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC,CD.
(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标;
(3)点M在y轴上且位于点C上方,点N在直线BC上,点P为第一象限内抛物线上一点,若以点C,M,N,P为顶点的四边形是菱形,求菱形的边长.

【答案】(1)![]() ;(2)E(1,
;(2)E(1,![]() ),(3,
),(3,![]() );(3)
);(3)![]() .
.
【解析】
试题分析:(1)用待定系数法求出抛物线解析式即可.
(2)分①点E在直线CD上方的抛物线上和②点E在直线CD下方的抛物线上两种情况,用三角函数求解即可;
(3)分①CM为菱形的边和②CM为菱形的对角线,用菱形的性质进行计算;
试题解析:(1)∵抛物线![]() 的图象经过点A(﹣2,0),点B(4,0),点D(2,4),∴设抛物线解析式为y=a(x+2)(x﹣4),∴﹣8a=4,∴a=
的图象经过点A(﹣2,0),点B(4,0),点D(2,4),∴设抛物线解析式为y=a(x+2)(x﹣4),∴﹣8a=4,∴a=![]() ,∴抛物线解析式为y=
,∴抛物线解析式为y=![]() (x+2)(x﹣4),即
(x+2)(x﹣4),即![]() ;
;
(2)如图1,①点E在直线CD上方的抛物线上,记E′,连接CE′,过E′作E′F′⊥CD,垂足为F′,由(1)知,OC=4,∵∠ACO=∠E′CF′,∴tan∠ACO=tan∠E′CF′,∴![]() =
=![]() ,设线段E′F′=h,则CF′=2h,∴点E′(2h,h+4).∵点E′在抛物线上,∴
,设线段E′F′=h,则CF′=2h,∴点E′(2h,h+4).∵点E′在抛物线上,∴![]() ,∴h=0(舍)h=
,∴h=0(舍)h=![]() ,∴E′(1,
,∴E′(1,![]() ),②点E在直线CD下方的抛物线上,记E,同①的方法得,E(3,
),②点E在直线CD下方的抛物线上,记E,同①的方法得,E(3,![]() ),点E的坐标为(1,
),点E的坐标为(1,![]() ),(3,
),(3,![]() );
);

(3)①CM为菱形的边,如图2,在第一象限内取点P′,过点
P′作P′N′∥y轴,交BC于N′,过点P′作P′M′∥BC,交y轴于M′,∴四边形CM′P′N′是平行四边形,∵四边形CM′P′N′是菱形,∴P′M′=P′N′,过点P′作P′Q′⊥y轴,垂足为Q′,∵OC=OB,∠BOC=90°,∴∠OCB=45°,∴∠P′M′C=45°,设点P′(m,![]() ),在Rt△P′M′Q′中,P′Q′=m,P′M′=
),在Rt△P′M′Q′中,P′Q′=m,P′M′=![]() m,∵B(4,0),C(0,4),∴直线BC的解析式为y=﹣x+4,∵P′N′∥y轴,∴N′(m,﹣m+4),∴P′N′=
m,∵B(4,0),C(0,4),∴直线BC的解析式为y=﹣x+4,∵P′N′∥y轴,∴N′(m,﹣m+4),∴P′N′=![]() =
=![]() ,∴
,∴![]() ,∴m=0(舍)或m=
,∴m=0(舍)或m=![]() ,菱形CM′P′N′的边长为
,菱形CM′P′N′的边长为![]() =
=![]() .
.

②CM为菱形的对角线,如图3,在第一象限内抛物线上取点P,过点P作PM∥BC,交y轴于点M,连接CP,过点M作MN∥CP,交BC于N,∴四边形CPMN是平行四边形,连接PN交CM于点Q,∵四边形CPMN是菱形,∴PQ⊥CM,∠PCQ=∠NCQ,∵∠OCB=45°,∴∠NCQ=45°,∴∠PCQ=45°,∴∠CPQ=∠PCQ=45°,∴PQ=CQ,设点P(n,![]() ),∴CQ=n,OQ=n+2,∴
),∴CQ=n,OQ=n+2,∴![]() ,∴n=0(舍),∴此种情况不存在,∴菱形的边长为
,∴n=0(舍),∴此种情况不存在,∴菱形的边长为![]() .
.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】点P在x轴的下方,且距离x轴3个单位长度,距离y轴4个单位长度,则点P的坐标为( )
A. (4,-3) B. (3,-4)
C. (-3,-4)或(3,-4) D. (-4,-3)或(4,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衣,平均每天可售出20件,每件衬衣盈利40元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衣降价1元,商场平均每天可多售出2件.
(1)若商场平均每天盈利1200元,每件衬衣应降价多少元?
(2)若要使商场平均每天的盈利最多,每件衬衣应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程的两根分别是2和﹣3,则这个一元二次方程是( )
A.x2﹣6x+8=0
B.x2+2x﹣3=0
C.x2﹣x﹣6=0
D.x2+x﹣6=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查:
①调查一批灯泡的使用寿命;②调查全班同学的身高;③调查市场上某种食品的色素含量是否符合国家标准;④企业招聘,对应聘人员进行面试.其中符合用抽样调查的是( )
A. ①② B. ①③ C. ②④ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A. 如果a∥b,b∥c,那么a∥c
B. 锐角三角形中最大的角一定大于或等于60°
C. 两条直线被第三条直线所截,内错角相等
D. 矩形的对角线相等且互相平分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com