
����Ŀ����һ��һ·���ǶԹ�˿��֮·�Ĵ��к����������й����������ϵ�����ܣ������豸�ǡ�һ��һ·�����߹�������������Ʒ��ij��ҵ�ƻ������ס������ֵ����豸���ڣ������豸�ۼ�50ǧԪ/���������豸�ۼ�30ǧԪ/���������������豸��ҪA��B����ԭ�ϣ��������豸��ҪA��ԭ��4��/����B��ԭ��2��/�����������豸��ҪA��ԭ��3��/����B��ԭ��1��/������֪A��ԭ����120�֣�B��ԭ����50�֣�
��1����ΰ�������������ǡ��ʹA��B����ԭ��ȫ�����ꣿ��ʱ�ܲ�ֵ�Ƕ���ǧԪ��
��2����ʹ�����豸�ۼ�����10%���������豸�ۼ��½�10%������Ҫ������豸�������豸������25��������ΰ��żס��������豸��������ʹ�����ܲ�ֵ�ܴﵽ1375ǧԪ����ʱA��B����ԭ�ϻ�ʣ�¶��ٶ֣�
���𰸡�(1)�������ֲ�Ʒ15��,�������ֲ�Ʒ20������ǡ��ʹ����ԭ��ȫ������,��ʱ�ܲ�ֵ��135��Ԫ (2)�����������ֲ�Ʒ25��,ʹ�ܲ�ֵ��1375ǧԪ,A��ԭ�ϻ�ʣ��20��
����������������1�������������ֲ�Ʒx�����������ֲ�Ʒy�������ݵ�����ϵ�����������ֲ�Ʒ��Ҫ��A��ԭ�ϵĶ���+�������ֲ�Ʒ��Ҫ��A��ԭ�ϵĶ���=A��ԭ��120�������������ֲ�Ʒ��Ҫ��B��ԭ�ϵĶ���+�������ֲ�Ʒ��Ҫ��B��ԭ�ϵĶ���=B��ԭ��50���������г�������⼴����
��2���������ֲ�Ʒ����z�������������ֲ�Ʒ��z+25���������ݵ�����ϵ�����ֲ�Ʒ�IJ�ֵ+���ֲ�Ʒ�IJ�ֵ=�ܲ�ֵ1375ǧԪ���г�������⼴�ɣ�
�������1�����������ֲ�Ʒx�����������ֲ�Ʒy���������������
![]() �������
�������![]() ��
��
15��50+30��20 =750+600=1350��ǧԪ����1350ǧԪ=135��Ԫ��
�����������ֲ�Ʒ15�����������ֲ�Ʒ20������ǡ��ʹ����ԭ��ȫ����������ʱ�ܲ�ֵ��135��Ԫ��
��2�������ֲ�Ʒ����z�������������ֲ�Ʒ��z+25�����������������
��1+10%����50��z+25��+��1��10%����30z=1375�������z=0
��z+25=25��
Aԭ��ʣ����120-25��4=120-100=20 ��������
Bԭ��ʣ����50-25��2=50-50=0��������
���������������ֲ�Ʒ25����ʹ�ܲ�ֵ��1375ǧԪ��A��ԭ�ϻ�ʣ��20����B��ԭ��������������ʣ��0�֣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ͬѧ���˽��Լ�������ˮƽ������1�����������ʦ��ȫ��45��ѧ��������һ������ģ����ԣ��÷־�Ϊ���������ɼ�����Ϊ10�֣�1�������ίԱ������β��Գɼ���������ͳ��ͼ�ͷ��������£�
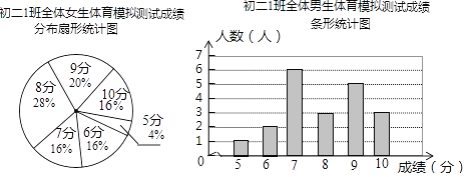
����1������ģ����Գɼ�������
ƽ���� | ���� | ��λ�� | ���� | |
���� | 2 | 8 | 7 | |
�� | 7.92 | 1.99 | 8 |
����������Ϣ������������⣺
��1������������________�ˣ�����Ů��________�ˣ�
��2����ȫ����1������ģ����Գɼ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ж���ʽ�ij˷��У�����ƽ���ʽ��������� ��
A. ��-m +n����m - n�� B. ��![]() a +b����b -
a +b����b -![]() a��
a��
C. ��x + 5����x + 5�� D. ��3a -4b����3b +4a��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AB�ǡ�O��ֱ������CD��AB�ڵ�E����PQ��AB����CD�ڵ�M��BE=18��CD=PQ=24����OM�ij�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C��������С����λ�ó������Σ��־���������С��֮����һ�����ﳬ�У�ʹ���е�����С���ľ�����ȣ�����Ӧ����( )

A. ��AC��BC���߸��ߵĽ��㴦
B. ��AC��BC�������ߵĽ��㴦
C. ��AC��BC���ߴ�ֱƽ���ߵĽ��㴦
D. ����A����B���ڽ�ƽ���ߵĽ��㴦
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O�İ뾶Ϊ3����ABC�ڽ��ڡ�O��AB=3 ![]() ��AC=3
��AC=3 ![]() ��D�ǡ�O��һ�㣬��AD=3����CD�ij�Ӧ�ǣ� ��
��D�ǡ�O��һ�㣬��AD=3����CD�ij�Ӧ�ǣ� ��
A.3
B.6
C.![]()
D.3��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����Կ����ڼ䣬�Ŷ��շѷ������£�������30��ʱ���˾��շ�120Ԫ������30���Ҳ�����m��30��m��100����ʱ��ÿ����1�ˣ��˾��շѽ���1Ԫ������m��ʱ���˾��շѶ�����m��ʱ�ı����辰��Ӵ���x���ο͵�ij�Ŷӣ���ȡ�ܷ���ΪyԪ��
��1����y����x�ĺ�������ʽ��
��2�����㹤����Ա���֣����Ӵ�ij�Ŷ���������һ������ʱ�����������������������ȡ���ܷ��÷���������һ����Ϊ������ȡ���ܷ��������Ŷ������������Ӷ����ӣ���m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��AD�ǽ�ƽ���ߣ�BEƽ�֡�ABC��AD�ڵ�E����O��AB�ϣ���OBΪ�뾶�ġ�O������E����AB�ڵ�F 
��1����֤��AD�ǡ�O�����ߣ�
��2����AC=4����C=30�㣬�� ![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com