练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    求证：三角形内角和等于180°．

    答案：
    解析：

    　　证明：过点A作EF∥BC，

    　　∴∠B＝∠1，∠C＝∠2(两直线平行，内错角相等)．

    　　∴∠1＋∠BAC＋∠2＝180°，

    　　∴∠B＋∠BAC＋∠C＝180°．

    　　思路点拨：先设出△ABC，∠A、∠B、∠C为三内角，如何证明∠A＋∠B＋∠C＝180°呢，我们用转化的思想把∠A，∠B，∠C的和转化为一个平角，如何转化呢？——可以通过△ABC的一个顶点作对边的平行线，再利用平行线的性质过哪个顶点呢？过哪个顶点都可．如下图．

    　　评注：①这是重要的数学事实，三角形内角和等于180°．

    　　②本题可以推广，四边形内角和可以分成两个三角形内角之和，如下图，所以四边形内角和为360°，n边形可以分成(n－2)个小三角形内角和，所以n边形内角和为(n－2)×180°．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    22、填空，完成下列证明过程．
    如图，△ABC中，∠B=∠C，D，E，F分别在AB，BC，AC上，且BD=CE，∠DEF=∠B，
    求证：ED=EF．
    证明：∵∠DEC=∠B+∠BDE（
    三角形的一个外角等于与它不相邻两个内角的和
    ），
    又∵∠DEF=∠B（已知），
    ∴∠
    BDE
    =∠
    CEF
    （等式性质）．
    在△EBD与△FCE中，
    ∠
    BDE
    =∠
    CEF
    （已证），
    BD
    =
    CE
    （已知），
    ∠B=∠C（已知），
    ∴△EBD≌△FCE（ASA）．
    ∴ED=EF（全等三角形的对应边相等）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

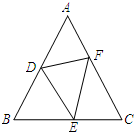    填空，完成下列证明过程．
    如图，△ABC中，∠B=∠C，D，E，F分别在AB，BC，AC上，且BD=CE，∠DEF=∠B
    求证：ED=EF．
    证明：∵∠DEC=∠B+∠BDE
    三角形的一个外角等于与它不相邻两个内角的和
    三角形的一个外角等于与它不相邻两个内角的和
    ，
    又∵∠DEF=∠B（已知），∴∠
    BDE
    BDE
    =∠
    CEF
    CEF
    （等式性质）．
    在△EBD与△FCE中，
    ∠
    BDE
    BDE
    =∠
    CEF
    CEF
    （已证），
    BD
    BD
    =
    CE
    CE
    （已知），∠B=∠C（已知），
    ∴△EBD≌△FCE
    ASA
    ASA
    ．
    ∴ED=EF
    全等三角形对应边相等
    全等三角形对应边相等
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：047

    如图，在△ABC中，∠BAC与∠ABC的平分线AE、BE相交于点E，延长AE交△ABC外接圆于D，连结BD、CD、CE，且∠BDA = 60o.

    求证：△BDE是等边三角形.

    撓旅媸切∨艉托∶鞯慕馓馑悸罚?/P>

    　　他们都用到了三角形的外角与内角的关系，及AE、BE的性质，但小鹏是先证∠DBE=∠DEB；再由∠BDA=60o 得△BDE是等边三角形；小明还用了三角形的内角和，算得∠BED=60o，再由∠BDA=60o 得△BDE是等边三角形.

    王老师的评价是：他们的思路都很好. ?/P>

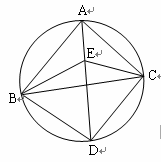
    现请你完成本题的证明，只要求写出一种证法，可参考他们的思路。

    查看答案和解析>>

    同步练习册答案