
 的图象与x轴交于点A.与
的图象与x轴交于点A.与 轴交于点
轴交于点 ;二次函数
;二次函数 图象与一次函数y=
图象与一次函数y= 的图象交于
的图象交于 、
、 两点,与
两点,与 轴交于
轴交于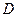 、
、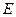 两点且
两点且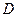 的坐标为
的坐标为

 轴上是否存在点P,使得△
轴上是否存在点P,使得△ 是直角三角形?若存在,求出所有的点
是直角三角形?若存在,求出所有的点 ,若不存在,请说明理由。
,若不存在,请说明理由。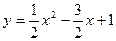
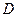 点的坐标为
点的坐标为 当x=1时, y=0
当x=1时, y=0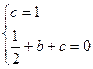 解得
解得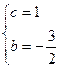 ,…………3分
,…………3分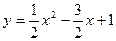 …………4分
…………4分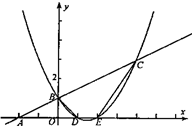
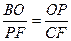 .即
.即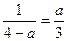 , …………5分
, …………5分

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:单选题
| A.y=-2x+3 | B.y=-2x-3 | C.y=2x+3 | D.y=x+3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 只叠放高度为
只叠放高度为 厘米,经实验发现,当叠放这种碗5只时,叠放高度为12厘米;当叠放这种碗8只时,叠放高度为15.6厘米。求
厘米,经实验发现,当叠放这种碗5只时,叠放高度为12厘米;当叠放这种碗8只时,叠放高度为15.6厘米。求 (厘米)与
(厘米)与 (只)之间的函数关系,并指出这种碗的深度是多少?
(只)之间的函数关系,并指出这种碗的深度是多少?
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 中,直线
中,直线 与两坐标轴围成一个△AOB.现将背面完全相同,正面分别标有数1、2、3、
与两坐标轴围成一个△AOB.现将背面完全相同,正面分别标有数1、2、3、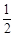 、
、 的5张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,将该数的倒数作为点P的纵坐标,则点P落在△AOB内的概率为 .
的5张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,将该数的倒数作为点P的纵坐标,则点P落在△AOB内的概率为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com