
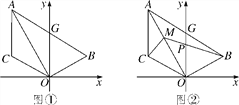
【题目】如图①,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴于G,连接OB,OC.
(1)判断△AOG的形状,并予以证明;
(2)若点B,C关于y轴对称,求证:AO⊥BO;
(3)在(2)的条件下,如图②,点M为OA上一点,且∠ACM=45°,BM交y轴于P,若点B的坐标为(3,1),求点M的坐标.
【答案】(1)△AOG是等腰三角形;(2)见解析;(3)M(-1,3).
【解析】
(1)、利用已知条件可证明∠GOA=∠GAO,由等腰三角形的判定可得AG=OG,所以△AOG是等腰三角形;(2)、由已知可得BP=CP,因为AC∥y轴,可得GA=GB;根据等腰三角形的性质得出∠GOB=∠GBO,∠AOG=∠OAG,所以∠AOG+∠BOG=∠OAG+∠OBG,即∠AOB=∠OAG+∠OBG,即可求得∠AOB=90°;(2)、先证得BM是∠ABC的平分线,设∠OBC=x,则x+∠POB=90°,而∠POA+∠POB=∠AOB=90°,求得x=∠POA,进一步证得x=∠GAM.根据∠OMB=∠GAM+∠ABM=x+∠ABM=x+∠PBM=∠MBO,得出OB=OM,然后证明出△OMF和△BOH全等,根据点B的坐标得出点M的坐标.
(1)解:△AOG的形状是等腰三角形
证明如下:∵AC∥y轴,∴∠CAO=∠GOA, ∵AO平分∠BAC,∴∠CAO=∠GAO,
∴∠GOA=∠GAO,∴AG=OG,∴△AOG是等腰三角形.
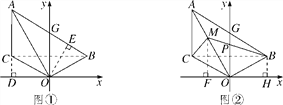
(2)证明:如图①,连接BC,过点O作OE⊥AB于点E,过点C作CD⊥x轴于点D.
∵B,C关于y轴对称,AC∥y轴,∴OB=OC,AC⊥BC,∴点A,C,D在同一条直线上.
∵AO为∠CAB的平分线,∴OD=OE.
在Rt△COD和Rt△BOE中,OD=OE,OC=OB,∴△COD≌△BOE(HL),∴∠DCO=∠EBO.
∵∠DCO+∠ACO=180°,∴在四边形ACOB中,∠ACO+∠EBO=180°,
∴∠BAC+∠BOC=180°, 设∠BAO=∠CAO=x,∠OBC=∠OCB=y,
∴2x+∠BOC=180°,2y+∠BOC=180°,∴x=y, ∴∠OAC=∠OBC,
∴∠AOB=∠ACB=90°,∴AO⊥OB.
(3)解:如图②,连接BC,过点M作MF⊥x轴于F,过点B作BH⊥x轴于H,
由(2)可知∠ACB=90°, ∵∠ACM=45°,∴CM平分∠ACB,
又∵AM平分∠BAC,∴BM平分∠ABC.设∠ABM=∠CBM=z,
由(2)可得∠OMB=x+z,∠OBM=y+z=x+z,∴∠OMB=∠OBM,∴OM=OB,
∴△OBM为等腰直角三角形. ∵∠BOH+∠MOF=90°,∠MOF+∠FMO=90°,
∴∠FMO=∠BOH,
在△OMF和△BOH中,∠MFO=∠OHB=90°,∠FMO=∠HOB,OM=OB,∴△OMF≌△BOH(AAS).
又∵点B的坐标为(3,1),∴OF=BH=1,MF=OH=3,∴M(-1,3).


科目:初中数学 来源: 题型:
【题目】保护环境、低碳出行已渐渐成为人们的习惯.最近无为县城又引进了共享单车,只需要交点押金,就可以通过扫描二维码的方式解锁一辆停在路边的自行车,以极低的费用,轻松骑到目的地.王老师家与学校相距2km,现在每天骑共享单车到学校所花的时间比过去骑电动车多用4min.已知王老师骑电动车的速度是骑共享单车速度的1.5倍,则王老师骑共享单车的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以线段AC为对角线的四边形ABCD(它的四个顶点A,B,C,D按顺时针方向排列),已知AB=BC=CD,∠ABC=100°,∠CAD=40°,则∠BCD的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,七(2)班的张明、王强等同学随家长一同到某公园游玩,下面是购买门票时,张明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
⑴张明他们一共去了几个成人,几个学生?
⑵请你帮助张明算一算,用哪种方式购票(团体购票还是非团体购票)更省钱?说明理由.
⑶正要购票时,张明发现七(3)班的张小毛等15名同学和他们的2名家长共17人也来购票,请你为他们设计出最省的购票方案,并求出此时的购票费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
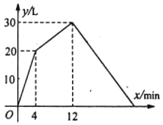
【题目】一个装有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单价:min)之间的关系如图所示。在第_______分钟时该容器内的水恰好为10L.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1是关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根,记△=b2﹣4ac,M=(2ax1+b)2 , 则关于△与M大小关系的下列说法中,正确的是( )
A.△>M
B.△=M
C.△<M
D.无法确定△与M的大小
查看答案和解析>>
科目:初中数学 来源: 题型:
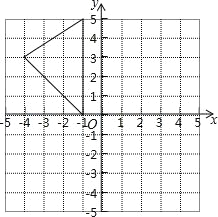
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com