
【题目】如图1,在Rt△ACB中,∠ACB=90°,∠ABC=30°,AC=1,点D为AC上一动点,连接BD,以BD为边作等边△BDE,设CD=n. 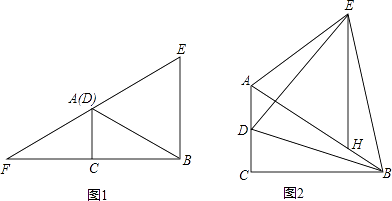
(1)当n=1时,EA的延长线交BC的延长线于F,则AF=;
(2)当0<n<1时,如图2,在BA上截取BH=AD,连接EH.
①设∠CBD=x,用含x的式子表示∠ADE和∠ABE.
②求证:△AEH为等边三角形.
【答案】
(1)2
(2)解:①证明:∵△BDE是等边三角形,
∴BE=BD,∠EDB=∠EBD=60°,
在△BCD中,∠ADE+∠EDB=∠CBD+∠C,
即∠ADE+60°=∠CBD+90°=x+90°,
∴∠ADE=30°+∠CBD,
∵∠HBE+∠ABD=60°,∠CBD+∠ABD=30°,
∴∠HBE=30°+∠CBD,
∴∠ADE=∠HBE,
∴∠ABE=∠ADE=x+90°;
②在△ADE与△HBE中,
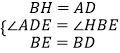 ,
,
∴△ADE≌△HBE(SAS),
∴AE=HE,∠AED=∠HEB,
∴∠AED+∠DEH=∠DEH+∠HEB,
即∠AEH=∠BED=60°,
∴△AEH为等边三角形
【解析】(1)解:∵△BDE是等边三角形,
∴∠EDB=60°,
∵∠ACB=90°,∠ABC=30°,
∴∠BAC=180°﹣90°﹣30°=60°,
∴FAC=180°﹣60°﹣60°=60°,
∴∠F=180°﹣90°﹣60°=30°,
∵∠ACB=90°,
∴∠ACF=180°﹣90°,
∴AF=2AC=2×1=2;
故答案为:2.
(1)根据三角形内角和定理求出∠BAC=60°,再根据平角等于180°求出∠FAC=60°,然后求出∠F=30°,根据30°角所对的直角边等于斜边的一半求解即可;(2)①根据三角形的任意一个外角等于与它不相邻的两个内角的和利用∠CBD表示出∠ADE=30°+∠CBD,又∠HBE=30°+∠CBD,从而得到∠ADE=∠ABE;②然后根据边角边证明△ADE与△HBE全等,根据全等三角形对应边相等可得AE=HE,对应角相等可得∠AED=∠HEB,然后推出∠AEH=∠BED=60°,再根据等边三角形的判定即可证明.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把△ABC经过平移得到△A′B′C′,若A(1,m),B(4,2),点A的对应点A′(3,m+2),则点B对应点B′的标为( )
A.(6,5)
B.(6,4)
C.(5,m)
D.(6,m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=mx与双曲线y=![]() 相交于A、B两点,A点的坐标为(1,2)
相交于A、B两点,A点的坐标为(1,2)
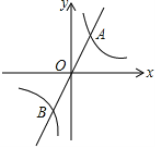
(1)求反比例函数的表达式;
(2)根据图象直接写出当mx>![]() 时,x的取值范围;
时,x的取值范围;
(3)计算线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市南县大力发展农村旅游事业,全力打造“洞庭之心湿地公园”,其中罗文村的“花海、涂鸦、美食”特色游享誉三湘,游人如织.去年村民罗南洲抓住机遇,返乡创业,投入20万元创办农家乐(餐饮+住宿),一年时间就收回投资的80%,其中餐饮利润是住宿利润的2倍还多1万元.
(1)求去年该农家乐餐饮和住宿的利润各为多少万元?
(2)今年罗南洲把去年的餐饮利润全部用于继续投资,增设了土特产的实体店销售和网上销售项目.他在接受记者采访时说:“我预计今年餐饮和住宿的利润比去年会有10%的增长,加上土特产销售的利润,到年底除收回所有投资外,还将获得不少于10万元的纯利润.”请问今年土特产销售至少有多少万元的利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于命题“已知:a∥b,b∥c,求证:a∥c”.如果用反证法,应先假设( )
A. a不平行b B. b不平行c C. a⊥c D. a不平行c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图,已知:∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为 . 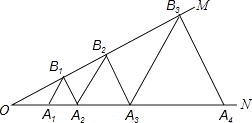
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com