

分析 根据不等式的解集,可得关于a,b的方程组,根据解方程组,可得a,b的值,根据负整数指数幂与正整数指数幂互为倒数,可得答案.
解答 解:$\left\{\begin{array}{l}{x≥-a-1①}\\{-x≥-b②}\end{array}\right.$,
由①得,x≥-a-1,
由②得,x≤b,
由数轴可得,原不等式的解集是:-2≤x≤3,
∴$\left\{\begin{array}{l}-a-1=-2\\ b=3\end{array}\right.$
∴$\left\{\begin{array}{l}a=1\\ b=3\end{array}\right.$,
b-a=${3^{-1}}=\frac{1}{3}$.
点评 本题考查了在数轴上表示不等式的解集,利用不等式的解集得出关于a,b的方程组是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
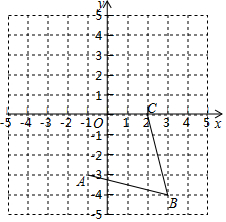 在正方形网格中,我们把每个小正方形的顶点叫做格点,连接任意两个格点的线段叫网格线段,以网格线段为边组成的图形叫做格点图形,如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.
在正方形网格中,我们把每个小正方形的顶点叫做格点,连接任意两个格点的线段叫网格线段,以网格线段为边组成的图形叫做格点图形,如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
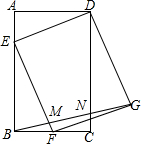 如图,在矩形ABCD中,AB=3,BC=2,点F是BC的中点,点E是边AB上一点,且BE=2,连结DE,EF,并以DE,EF为边作?EFGD,连结BG,分别交EF和DC于点M,N,则$\frac{BM}{NG}$=$\frac{6}{7}$.
如图,在矩形ABCD中,AB=3,BC=2,点F是BC的中点,点E是边AB上一点,且BE=2,连结DE,EF,并以DE,EF为边作?EFGD,连结BG,分别交EF和DC于点M,N,则$\frac{BM}{NG}$=$\frac{6}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com