
ЁОЬтФПЁПСНИіздгЩзЊЖЏЕФзЊХЬШчЭМЫљЪОЃЌвЛИіЗжЮЊ![]() ЕШЗнЃЌЗжБ№БъгаЪ§зж
ЕШЗнЃЌЗжБ№БъгаЪ§зж![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌСэвЛИіЗжЮЊ
ЃЌСэвЛИіЗжЮЊ![]() ЕШЗнЃЌЗжБ№БъгаЪ§зж
ЕШЗнЃЌЗжБ№БъгаЪ§зж![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎзЊХЬЩЯгаЙЬЖЈжИеыЃЌЭЌЪБзЊЖЏСНИізЊХЬЃЌЕБзЊХЬЭЃжЙзЊЖЏКѓЃЌжИеыжИЯђЕФЪ§зжМДЮЊзЊГіЕФЪ§зжЃЎМзЁЂввСНШЫжЦЖЈгЮЯЗЙцдђШчЯТЃКвЛШЫЯШВТЪ§ЃЌШЛКѓСэвЛШЫдйзЊЖЏзЊХЬЃЌШєВТГіЕФЪ§зжгызЊГіЕФСНИіЪ§зжжЎКЭЯрЕШЃЌдђВТЪ§ЕФШЫЛёЪЄЃЌЗёдђзЊЖЏзЊХЬЕФШЫЛёЪЄЃЎВТЪ§епПЩДгЯТУц
ЃЎзЊХЬЩЯгаЙЬЖЈжИеыЃЌЭЌЪБзЊЖЏСНИізЊХЬЃЌЕБзЊХЬЭЃжЙзЊЖЏКѓЃЌжИеыжИЯђЕФЪ§зжМДЮЊзЊГіЕФЪ§зжЃЎМзЁЂввСНШЫжЦЖЈгЮЯЗЙцдђШчЯТЃКвЛШЫЯШВТЪ§ЃЌШЛКѓСэвЛШЫдйзЊЖЏзЊХЬЃЌШєВТГіЕФЪ§зжгызЊГіЕФСНИіЪ§зжжЎКЭЯрЕШЃЌдђВТЪ§ЕФШЫЛёЪЄЃЌЗёдђзЊЖЏзЊХЬЕФШЫЛёЪЄЃЎВТЪ§епПЩДгЯТУц![]() ЃЌ
ЃЌ![]() СНжжЗНАИжабЁвЛжжЃКЗНАИ
СНжжЗНАИжабЁвЛжжЃКЗНАИ![]() ЃКВТЁАЦцЪ§ЁБЛђВТЁАХМЪ§ЁБЦфжаЕФвЛжжЃЛЗНАИ
ЃКВТЁАЦцЪ§ЁБЛђВТЁАХМЪ§ЁБЦфжаЕФвЛжжЃЛЗНАИ![]() ЃКВТЁАЪЧ
ЃКВТЁАЪЧ![]() ЕФећЪ§БЖЁБЛђВТЁАВЛЪЧ
ЕФећЪ§БЖЁБЛђВТЁАВЛЪЧ![]() ЕФећЪ§БЖЁБЦфжаЕФвЛжжЃЎ
ЕФећЪ§БЖЁБЦфжаЕФвЛжжЃЎ
![]() ШчЙћФуЪЧВТЪ§ЕФгЮЯЗепЃЌЮЊСЫОЁПЩФмЛёЪЄЃЌФуНЋбЁдёФФжжЗНАИЃЌВТИУжжЗНАИжаЕФФФвЛжжЧщПіЃПЧыЫЕУїРэгЩЃЛ
ШчЙћФуЪЧВТЪ§ЕФгЮЯЗепЃЌЮЊСЫОЁПЩФмЛёЪЄЃЌФуНЋбЁдёФФжжЗНАИЃЌВТИУжжЗНАИжаЕФФФвЛжжЧщПіЃПЧыЫЕУїРэгЩЃЛ
![]() ЮЊСЫБЃжЄВЮгыгЮЯЗЫЋЗНЕФЙЋЦНадЃЌФугІбЁдёФФжжВТЪ§ЕФЗНАИЃПЮЊЪВУДЃП
ЮЊСЫБЃжЄВЮгыгЮЯЗЫЋЗНЕФЙЋЦНадЃЌФугІбЁдёФФжжВТЪ§ЕФЗНАИЃПЮЊЪВУДЃП
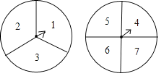
ЁОД№АИЁП![]() ЮвбЁдё
ЮвбЁдё![]() ЕФВТЪ§ЕФЗНАИЃЌВЂЧвВТЁАКЭВЛЪЧ
ЕФВТЪ§ЕФЗНАИЃЌВЂЧвВТЁАКЭВЛЪЧ![]() ЕФећЪ§БЖЁБЃЌвђЮЊДЫЪБЛёЪЄЕФИХТЪЮЊ
ЕФећЪ§БЖЁБЃЌвђЮЊДЫЪБЛёЪЄЕФИХТЪЮЊ![]() ЃЌЛёЪЄЕФПЩФмадзюДѓЃЛ
ЃЌЛёЪЄЕФПЩФмадзюДѓЃЛ![]() ЮЊСЫБЃжЄгЮЯЗЕФЙЋЦНадЃЌгІИУбЁдёЗНАИ
ЮЊСЫБЃжЄгЮЯЗЕФЙЋЦНадЃЌгІИУбЁдёЗНАИ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉСаОйГіЫљгаЧщПіЃЌЗжБ№ЕУЕНЯргІЕФИХТЪЃЌБШНЯМДПЩЃЛ
ЃЈ2ЃЉгІбЁдёЛёЪЄИХТЪЯрЭЌЕФгЮЯЗНјЖјЕУГіД№АИЃЎ
![]() бЁдё
бЁдё![]() ЕФВТЪ§ЕФЗНАИЃЌВЂЧвВТЁАКЭВЛЪЧ
ЕФВТЪ§ЕФЗНАИЃЌВЂЧвВТЁАКЭВЛЪЧ![]() ЕФећЪ§БЖЁБЃЎ
ЕФећЪ§БЖЁБЃЎ
СаЪїзДЭМШчЯТЃК
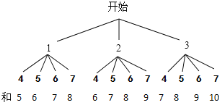
ЙВга![]() жжПЩФмНсЙћЃЌЧвУПжжНсЙћГіЯжЕФПЩФмадЯрЭЌЃЎ
жжПЩФмНсЙћЃЌЧвУПжжНсЙћГіЯжЕФПЩФмадЯрЭЌЃЎ
ЗНАИ![]() ЃКгЩЪїзДЭМПЩЕУЃЌКЭЮЊЦцЪ§вдМАКЭЮЊХМЪ§ЕФНсЙћЗжБ№ЪЧ
ЃКгЩЪїзДЭМПЩЕУЃЌКЭЮЊЦцЪ§вдМАКЭЮЊХМЪ§ЕФНсЙћЗжБ№ЪЧ![]() жжЃЌ
жжЃЌ
Ыљвд![]() ЃЈКЭЮЊЦцЪ§ЃЉ
ЃЈКЭЮЊЦцЪ§ЃЉ![]() ЃЛ
ЃЛ![]() ЃЈКЭЮЊХМЪ§ЃЉ
ЃЈКЭЮЊХМЪ§ЃЉ![]() ЃЛ
ЃЛ
ЗНАИ![]() ЃКгЩЪїзДЭМПЩЕУЃЌКЭЪЧ
ЃКгЩЪїзДЭМПЩЕУЃЌКЭЪЧ![]() ЕФећЪ§БЖга
ЕФећЪ§БЖга![]() жжЃЌМДЮЊ
жжЃЌМДЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
Ыљвд![]() ЃЈКЭЪЧ
ЃЈКЭЪЧ![]() ЕФећЪ§БЖЃЉ
ЕФећЪ§БЖЃЉ![]() ЃЛ
ЃЛ![]() ЃЈКЭВЛЪЧ
ЃЈКЭВЛЪЧ![]() ЕФећЪ§БЖЃЉ
ЕФећЪ§БЖЃЉ![]() ЃЎ
ЃЎ
ЫљвдЃЌЮвбЁдё![]() ЕФВТЪ§ЕФЗНАИЃЌВЂЧвВТЁАКЭВЛЪЧ
ЕФВТЪ§ЕФЗНАИЃЌВЂЧвВТЁАКЭВЛЪЧ![]() ЕФећЪ§БЖЁБЃЌвђЮЊДЫЪБЛёЪЄЕФИХТЪЮЊ
ЕФећЪ§БЖЁБЃЌвђЮЊДЫЪБЛёЪЄЕФИХТЪЮЊ![]() ЃЌЛёЪЄЕФПЩФмадзюДѓЃЎ
ЃЌЛёЪЄЕФПЩФмадзюДѓЃЎ
![]() ЮЊСЫБЃжЄгЮЯЗЕФЙЋЦНадЃЌгІИУбЁдёЗНАИ
ЮЊСЫБЃжЄгЮЯЗЕФЙЋЦНадЃЌгІИУбЁдёЗНАИ![]() ЃЎ
ЃЎ
вђЮЊ![]() ЃЈКЭЮЊЦцЪ§ЃЉ
ЃЈКЭЮЊЦцЪ§ЃЉ![]() ЃЈКЭЮЊХМЪ§ЃЉ
ЃЈКЭЮЊХМЪ§ЃЉ![]() ЃЌ
ЃЌ
ЫљвдЃЌбЁдёЗНАИ![]() ЕФВТЪ§ЗНЗЈЖдЫЋЗНЪЧЙЋЦНЕФЃЎ
ЕФВТЪ§ЗНЗЈЖдЫЋЗНЪЧЙЋЦНЕФЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЃКADЦНЗжЁЯCAEЃЌADЁЮBCЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABCЪЧЕШбќШ§НЧаЮЃЎ
ЃЈ2ЃЉЕБЁЯCAEЕШгкЖрЩйЖШЪБЁїABCЪЧЕШБпШ§НЧаЮЃПжЄУїФуЕФНсТлЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
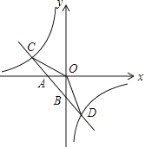
ЁОЬтФПЁПШчЭМЃЌвбжЊвЛДЮКЏЪ§![]() ЕФЭМЯѓгыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌгыЗДБШР§КЏЪ§
ЕФЭМЯѓгыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓЗжБ№НЛгкCЁЂDСНЕуЃЌЕуDЃЈ2ЃЌЉ3ЃЉЃЌЕуAЃЈ-2ЃЌ0ЃЉЃЎ
ЕФЭМЯѓЗжБ№НЛгкCЁЂDСНЕуЃЌЕуDЃЈ2ЃЌЉ3ЃЉЃЌЕуAЃЈ-2ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§![]() гыЗДБШР§КЏЪ§
гыЗДБШР§КЏЪ§![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЁїCODЕФУцЛ§ЃЛ
ЃЈ3ЃЉжБНгаДГіy1ЃОy2ЪБздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCКЭЁїCEFОљЮЊЕШбќжБНЧШ§НЧаЮЃЌEдкЁїABCФкЃЌЁЯCAE+ЁЯCBE=90ЁуЃЌСЌНгBFЃЎ

ЁЁ (1)ЧѓжЄЃКЁїCAEЁзЁїCBF
(2)ШєBE=1ЃЌAE=2ЃЌЧѓCEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
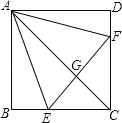
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌЕуEЁЂFЗжБ№дкBCЁЂCDЩЯЃЌЁїAEFЪЧЕШБпШ§НЧаЮЃЌСЌНгACНЛEFгкGЃЌЯТСаНсТлЃКЂйBE=DFЃЌЂкЁЯDAF=15ЁуЃЌЂлACДЙжБЦНЗжEFЃЌЂмBE+DF=EFЃЌЂнSЁїCEF=2SЁїABEЃЎЦфжае§ШЗНсТлга____ЃЎЃЈЬюађКХМДПЩЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌADЁЮBCЃЌЁЯA=90ЁуЃЌAD=1cmЃЌAB=3cmЃЌBC=5cmЃЌЖЏЕуPДгЕуBГіЗЂвд1cm/sЕФЫйЖШбиBCЕФЗНЯђдЫЖЏЃЌЖЏЕуQДгЕуCГіЗЂвд2cm/sЕФЫйЖШбиCDЗНЯђдЫЖЏЃЌPЁЂQСНЕуЭЌЪБГіЗЂЃЌЕБQЕНДяЕуDЪБЭЃжЙдЫЖЏЃЌЕуPвВЫцжЎЭЃжЙЃЌЩшдЫЖЏЕФЪБМфЮЊtsЃЈtЃО0ЃЉ
ЃЈ1ЃЉЧѓЯпЖЮCDЕФГЄЃЛ
ЃЈ2ЃЉtЮЊКЮжЕЪБЃЌЯпЖЮPQНЋЫФБпаЮABCDЕФУцЛ§ЗжЮЊ1ЃК2СНВПЗжЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌЖЅЕузјБъЃЈ1ЃЌnЃЉЃЌгыyжсЕФНЛЕудкЃЈ0ЃЌ3ЃЉЃЌЃЈ0ЃЌ4ЃЉжЎМфЃЈАќКЌЖЫЕуЃЉЃЌдђЯТСаНсТлЃКЂйabcЃО0ЃЛЂк3a+bЃМ0ЃЛЂлЉ
гыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌЖЅЕузјБъЃЈ1ЃЌnЃЉЃЌгыyжсЕФНЛЕудкЃЈ0ЃЌ3ЃЉЃЌЃЈ0ЃЌ4ЃЉжЎМфЃЈАќКЌЖЫЕуЃЉЃЌдђЯТСаНсТлЃКЂйabcЃО0ЃЛЂк3a+bЃМ0ЃЛЂлЉ![]() ЁмaЁмЉ1ЃЛЂмa+bЁнam2+bmЃЈmЮЊШЮвтЪЕЪ§ЃЉЃЛЂнвЛдЊЖўДЮЗНГЬ
ЁмaЁмЉ1ЃЛЂмa+bЁнam2+bmЃЈmЮЊШЮвтЪЕЪ§ЃЉЃЛЂнвЛдЊЖўДЮЗНГЬ![]() гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЦфжае§ШЗЕФгаЃЈЁЁЁЁЃЉ
гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЦфжае§ШЗЕФгаЃЈЁЁЁЁЃЉ

A. 2Иі B. 3Иі C. 4Иі D. 5Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCКЭЁїCDEОљЮЊЕШбќжБНЧШ§НЧаЮЃЌЕуBЃЌCЃЌDдквЛЬѕжБЯпЩЯЃЌЕуMЪЧAEЕФжаЕуЃЌЯТСаНсТлЃКЂйtanЁЯAEC=![]() ЃЛЂкSЁїABC+SЁїCDEЈRSЁїACEЃЛЂлBMЁЭDMЃЛЂмBM=DMЃЌе§ШЗНсТлЕФИіЪ§ЪЧЃЈ ЃЉ
ЃЛЂкSЁїABC+SЁїCDEЈRSЁїACEЃЛЂлBMЁЭDMЃЛЂмBM=DMЃЌе§ШЗНсТлЕФИіЪ§ЪЧЃЈ ЃЉ
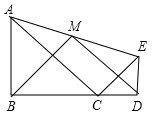
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСРэНтВФСЯвЛЃКвЛзщЖдБпЦНааЃЌСэвЛзщЖдБпВЛЦНааЕФЫФБпаЮНаЬнаЮЃЌЦфжаЦНааЕФСНБпНаЬнаЮЕФЕзБпЃЌВЛЦНааЕФСНБпНаЬнаЮЕФЕзБпЃЌВЛЦНааЕФСНБпНаЬнаЮЕФбќЃЌСЌНгЬнаЮСНбќжаЕуЕФЯпЖЮНаЬнаЮЕФжаЮЛЯпЃЎЬнаЮЕФжаЮЛЯпОпгавдЯТаджЪЃКЬнаЮЕФжаЮЛЯпЦНаагкСНЕзКЭЃЌВЂЧвЕШгкСНЕзКЭЕФвЛАыЃЎ
ШчЭМЃЈ1ЃЉЃКдкЬнаЮABCDжаЃКADЁЮBCЃЌ
ЁпEЁЂFЪЧABЁЂCDЕФжаЕуЃЌЁрEFЁЮADЁЮBCЃЌEF=![]() ЃЈAD+BCЃЉ
ЃЈAD+BCЃЉ
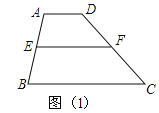
ВФСЯЖўЃКОЙ§Ш§НЧаЮвЛБпЕФжаЕугыСэвЛБпЦНааЕФжБЯпБиЦНЗжЕкШ§Бп
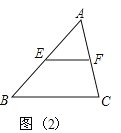
ШчЭМЃЈ2ЃЉЃКдкЁїABCжаЃКЁпEЪЧABЕФжаЕуЃЌEFЁЮBC
ЁрFЪЧACЕФжаЕу
ЧыФудЫгУЫљбЇжЊЪЖЃЌНсКЯЩЯЪіВФСЯЃЌНтД№ЯТСаЮЪЬтЃЎ
ШчЭМЃЈ3ЃЉдкЬнаЮABCDжаЃЌADЁЮBCЃЌACЁЭBDгкOЃЌEЁЂFЗжБ№ЮЊABЁЂCDЕФжаЕуЃЌЁЯDBC=30ЁуЃЎ
ЃЈ1ЃЉЧѓжЄЃКEF=ACЃЛ
ЃЈ2ЃЉШєOD=![]() ЃЌOC=5ЃЌЧѓMNЕФГЄЃЎ
ЃЌOC=5ЃЌЧѓMNЕФГЄЃЎ
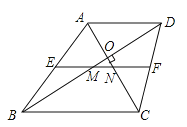
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com