
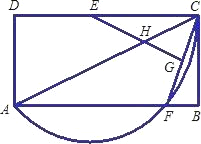
【题目】已知:如图,矩形ABCD中,点E、F分别在DC,AB边上,且点A、F、C在以点E为圆心,EC为半径的圆上,连接CF,作EG⊥CF于G,交AC于H.已知AB=6,设BC=x,AF=y.
(1)求证:∠CAB=∠CEG;
(2)①求y与x之间的函数关系式. ②x= 时,点F是AB的中点;
(3)当x为何值时,点F是![]() 的中点,以A、E、C、F为顶点的四边形是何种特殊四边形?试说明理由.
的中点,以A、E、C、F为顶点的四边形是何种特殊四边形?试说明理由.
【答案】(1)证明见解析(2)①y=﹣![]() x2+6②3
x2+6②3![]() (3)2
(3)2![]()
【解析】
(1)连接EF,由于EG经过圆心E,且与弦CF垂直,由垂径定理知∠CEF=2∠CEG,而圆周角∠CAF和圆心角∠CEG所对的弧正好相同,由圆周角定理知∠CEG=2∠CAF,由此得证;
(2)①设⊙O的半径为r,连接EA、EF;由于EA=EF,那么E点在AF的垂直平分线上,因此AF=2DE,即y=2(6﹣r),所以只需求出r、x的关系式即可;Rt△ADE中,AD=x,用r可表示出AE、DE的长,即可由勾股定理求得r、x的关系式,由此得解;②当F是AB中点时,AF=y=3,将其代入①的函数关系式中,即可求得x的值;
(3)当F是弧AC的中点时,EF垂直平分AC,可得AE=EC,AF=FC;易知∠AEF=∠CEF,而∠CEF和∠AFE是平行线的内错角,等量代换后可得∠AEF=∠AFE=∠FAE,由此可证得△EAF是正三角形,由此可证得四边形AECF的四边都相等,即四边形AECF是菱形;此时∠CFB=∠EAF=60°,在Rt△CFB中,易知BF=![]() CF,而AF=FC,那么BF即为AF的一半、AB的三分之一,由此可求得BF的长,进而可得到BC(即x)的长.
CF,而AF=FC,那么BF即为AF的一半、AB的三分之一,由此可求得BF的长,进而可得到BC(即x)的长.
(1)连接EF(如图1),
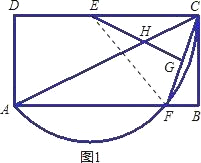
∵点A、F、C在以点E为圆心,EC为半径的圆上,
∴EF=EC,
∵EG⊥CF,
∴∠CEF=2∠CEG,
∵∠CEF=2∠CAB,∴∠CAB=∠CEG;
(2)(如图2)①连接EF、EA,

设⊙E的半径为r,
在Rt△ADE中,EA=r,DE=6﹣r,AD=x,
∴x2+(6﹣r)2=r2,r=![]() x2+3,
x2+3,
∵EF=EA,
∴AF=2DE,
即y=2(6﹣r)=﹣![]() x2+6;
x2+6;
②点F是AB的中点时,y=3,即﹣![]() x2+6=3,
x2+6=3,
∴x=![]() ;
;
(3)(如图3)
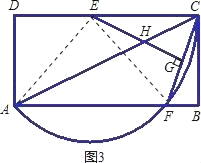
当x=![]() 时,F是弧AC的中点.此时四边形AECF菱形;
时,F是弧AC的中点.此时四边形AECF菱形;
理由如下:
∵点F是弧AC的中点,
∴∠AEF=∠CEF,AF=CF,
∵AB∥CD,
∴∠AFE=∠CEF,
∴∠AEF=∠AFE,
∴AE=AF,
∵AE=EF,
∴AE=AF=CE=CF,
∴△AEF和△CEF都是正三角形,
∴四边形AECF是菱形,且∠CEF=60°,
∴∠BCF=30°,∴BF=![]() CF=
CF=![]() AF=
AF=![]() AB=2,BC=
AB=2,BC=![]() .
.


科目:初中数学 来源: 题型:
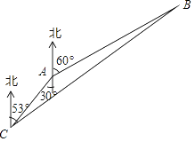
【题目】2016年12月底我国首艘航空母舰辽宁舰与数艘去驱航舰组成编队,携多架歼﹣15舰载战斗机和多型舰载直升机开展跨海区训练和试验任务,在某次演习中,预警直升机A发现在其北偏东60°,距离160千米处有一可疑目标B,预警直升机立即向位于南偏西30°距离40千米处的航母C报告,航母舰载战斗机立即升空沿北偏东53°方向向可疑目标飞去,请求出舰载战斗机到达目标的航程BC.
(结果保留整数,参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
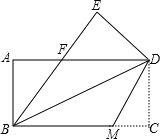
【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)若△ABC和△A1B1C1关于原点O成中心对称图形,画出△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2;
(3)在x轴上存在一点P,满足点P到点B1与点C1距离之和最小,请直接写出P B1+ P C1的最小值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
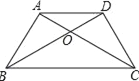
【题目】如图,已知梯形ABCD中,AD∥BC,AB=CD=AD,AC、BD相交于点O,∠BCD=60°,则下列4个结论:①梯形ABCD是轴对称图形;②BC=2AD;③梯形ABCD是中心对称图形;④AC平分∠DCB,其中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内有一点P,若PA=1,PB=2,PC=3.
(1)画出△ABP绕点B顺时针旋转90°得到的△CBE;
(2)求∠APB度数;
(3)求正方形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角体系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3。取BO的中点D,连接CD、MD和OC。

(1)求证:CD是⊙M的切线;
(2)二次函数的图象经过点D、M、A,其对称轴上有一动点P,连接PD、PM,求△PDM的周长最小时点P的坐标;
(3)在(2)的条件下,当△PDM的周长最小时,抛物线上是否存在点Q,使![]() ?若存在,求出点Q的坐标;若不存在,请说明理由。
?若存在,求出点Q的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
![]() 当点
当点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上时(如图
上时(如图![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,请探索
,请探索![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
![]() 当
当![]() ,
,
①点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,如图
上,如图![]() 时,请写出线段
时,请写出线段![]() 、
、![]() 之间的数量关系,并给予证明.
之间的数量关系,并给予证明.
②当点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 的延长线上,如图
的延长线上,如图![]() 时,请判断①中线段
时,请判断①中线段![]() 、
、![]() 之间的数量关系是否还存在.(直接写出答案,不用证明)
之间的数量关系是否还存在.(直接写出答案,不用证明)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com