
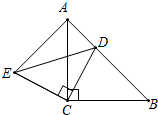
 △ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上.
△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上.| 3 |
|
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
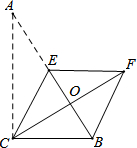
 “三月三,放风筝”,这天,妈妈让小玉自己动手制作一个如图所示的小风筝,它由两个三角形拼成,而且要满足△ABC≌△ADE才符合要求,小玉通过测量得到AB=AD,∠BAE=∠DAC,为了保证符合要求,还需要测量哪一对相等的量?请你帮助小玉找出一对相等的量并说明理由.
“三月三,放风筝”,这天,妈妈让小玉自己动手制作一个如图所示的小风筝,它由两个三角形拼成,而且要满足△ABC≌△ADE才符合要求,小玉通过测量得到AB=AD,∠BAE=∠DAC,为了保证符合要求,还需要测量哪一对相等的量?请你帮助小玉找出一对相等的量并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
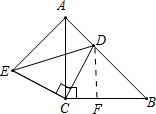
 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=3,点E是AB的中点.将△ACE沿CE折叠后得到△CEF,点A落在F点处,CF交AB于点O,连结BF,则四边形BCEF的面积是
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=3,点E是AB的中点.将△ACE沿CE折叠后得到△CEF,点A落在F点处,CF交AB于点O,连结BF,则四边形BCEF的面积是查看答案和解析>>
科目:初中数学 来源: 题型:
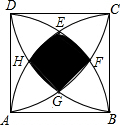 如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为( )
如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为( )A、
| ||
B、
| ||
| C、π | ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com