
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足 ![]() ,过C作CB⊥x轴于B.
,过C作CB⊥x轴于B.
(1)求△ABC的面积.
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
(3)在y轴上是否存在点P,使得△ABC和△ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
【答案】
(1)
解:∵(a+2)2+ ![]() =0,
=0,
∴a=2=0,b﹣2=0,
∴a=﹣2,b=2,
∵CB⊥AB
∴A(﹣2,0),B(2,0),C(2,2),
∴△ABC的面积= ![]() ×2×4=4
×2×4=4
(2)
解:∵CB∥y轴,BD∥AC,
∴∠CAB=∠5,∠ODB=∠6,∠CAB+∠ODB=∠5+∠6=90°,
过E作EF∥AC,如图①,
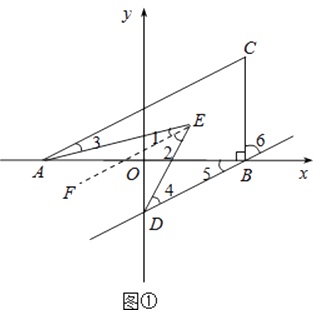
∵BD∥AC,
∴BD∥AC∥EF,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠3= ![]() ∠CAB=∠1,∠4=
∠CAB=∠1,∠4= ![]() ∠ODB=∠2,
∠ODB=∠2,
∴∠AED=∠1+∠2= ![]() (∠CAB+∠ODB)=45°
(∠CAB+∠ODB)=45°
(3)
解:①当P在y轴正半轴上时,如图②,
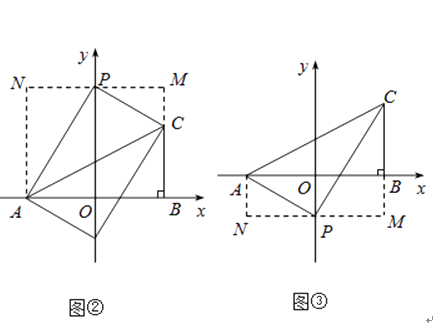
设P(0,t),
过P作MN∥x轴,AN∥y轴,BM∥y轴,
∵S△APC=S梯形MNAC﹣S△ANP﹣S△CMP=4,
∴ ![]() ﹣t﹣(t﹣2)=4,解得t=3,
﹣t﹣(t﹣2)=4,解得t=3,
②当P在y轴负半轴上时,如图③
∵S△APC=S梯形MNAC﹣S△ANP﹣S△CMP=4
∴ ![]() +t﹣(2﹣t)=4,解得t=﹣1,
+t﹣(2﹣t)=4,解得t=﹣1,
∴P(0,﹣1)或(0,3)
【解析】(1)根据非负数的性质易得a=﹣2,b=2,然后根据三角形面积公式计算;(2)过E作EF∥AC,根据平行线性质得BD∥AC∥EF,且∠3= ![]() ∠CAB=∠1,∠4=
∠CAB=∠1,∠4= ![]() ∠ODB=∠2,所以∠AED=∠1+∠2=
∠ODB=∠2,所以∠AED=∠1+∠2= ![]() (∠CAB+∠ODB);然后把∠CAB+∠ODB=∠5+∠6=90° 代入计算即可;(3)分类讨论:设P(0,t),当P在y轴正半轴上时,过P作MN∥x轴,AN∥y轴,BM∥y轴,利用S△APC=S梯形MNAC﹣S△ANP﹣S△CMP=4可得到关于t的方程,再解方程求出t;
(∠CAB+∠ODB);然后把∠CAB+∠ODB=∠5+∠6=90° 代入计算即可;(3)分类讨论:设P(0,t),当P在y轴正半轴上时,过P作MN∥x轴,AN∥y轴,BM∥y轴,利用S△APC=S梯形MNAC﹣S△ANP﹣S△CMP=4可得到关于t的方程,再解方程求出t;
当P在y轴负半轴上时,运用同样方法可计算出t.
【考点精析】掌握平行线的判定与性质和三角形的面积是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;三角形的面积=1/2×底×高.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元,170元的A、B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
求A、B两种型号的电风扇的销售单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》勾股章有一问题,其意思是:现有一竖立着的木柱,在木柱上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索退行,在离木柱根部8尺处时绳索用尽,请问绳索有多长?若设绳索长度为x尺,根据题意,可列方程为 ( )
A. 82﹢x2 = (x﹣3)2B. 82﹢(x+3)2= x2
C. 82﹢(x﹣3)2= x2D. x2﹢(x﹣3)2= 82
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某品牌电风扇销售量的情况,对某商场5月份该品牌甲、乙、丙三种型号的电风扇销售量进行统计,绘制如下两个统计图(均不完整).请你结合图中的信息,解答下列问题: 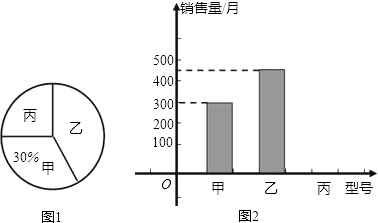
(1)该商场5月份售出这种品牌的电风扇共多少台?
(2)若该商场计划订购这三种型号的电风扇共2000台,根据5月份销售量的情况,求该商场应订购丙种型号电风扇多少台比较合理?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com