
【题目】请根据图示的对话解答下列问题.

求:(1)a,b的值;
(2)8﹣a+b﹣c的值.
【答案】 (1)a=-3,b=±7;(2)33或5.
【解析】
(1)首先根据相反数的概念求得a的值,根据绝对值求得b,b的值有了两个;
(2)根据b的两个取值,分别求出两个c的值,再分别代入8-a+b-c,求值即可.
解:(1)因为a的相反数是3,b的绝对值是7,
所以a=-3,b=±7;
(2)因为a=-3,b=±7,c和b的和是-8,
所以当b=7时,c= -15,
当b= -7时,c= -1,
当a=-3,b=7,c=-15时,8-a+b-c=8-(-3)+7-(-15)=33;
当a=-3,b=-7,c=-1时,8-a+b-c=8-(-3)+(-7)-(-1)=5.
故答案为:(1)a=-3,b=±7;(2)33或5.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,双曲线:y= ![]() (x>0)分别与直线OA:y=x和直线AB:y=﹣x+10,交于C,D两点,并且OC=3BD.
(x>0)分别与直线OA:y=x和直线AB:y=﹣x+10,交于C,D两点,并且OC=3BD. 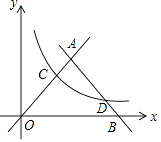
(1)求出双曲线的解析式;
(2)连结CD,求四边形OCDB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为一斜坡,其坡角为19.5°,紧挨着斜坡AB底部A处有一高楼,一数学活动小组量得斜坡长AB=15m,在坡顶B处测得楼顶D处的仰角为45°,其中测量员小刚的身高BC=1.7米,求楼高AD.
(参考数据:sin19.5°≈ ![]() ,tan19.5°≈
,tan19.5°≈ ![]() ,最终结果精确到0.1m).
,最终结果精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.
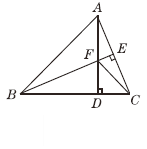
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线L1过A(0,2),B(2,0)两点,直线L2:y=mx+b过点C(1,0),且把△AOB分成两部分,其中靠近原点的那部分是一个三角形,设此三角形的面积为S,求S关于m的函数解析式,及自变量m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分类
﹣3,0.45, ![]() ,0,9,﹣1,﹣1
,0,9,﹣1,﹣1![]() ,10,﹣3.14
,10,﹣3.14
(1)正整数:{ …}
(2)负整数:{ …}
(3)整数:{ …}
(4)分数:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线C1:y=a(x+1)(x﹣3a)(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,﹣3)
(1)求抛物线C1的解析式及A,B点坐标;
(2)求抛物线C1的顶点坐标;
(3)将抛物线C1向上平移3个单位长度,再向左平移n(n>0)个单位长度,得到抛物线C2 , 若抛物线C2的顶点在△ABC内,求n的取值范围. (在所给坐标系中画出草图C1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(﹣1,y1),(4,y2)在一次函数y=3x﹣2的图象上,则y1 , y2 , 0的大小关系是( )
A.0<y1<y2
B.y1<0<y2
C.y1<y2<0
D.y2<0<y1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com