
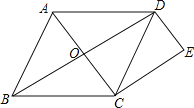
【题目】如图,点O是菱形ABCD对角线的交点,过点C作CE∥OD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形OCED是矩形.
(2)若AB=4,∠ABC=60°,求矩形OCED的面积.
【答案】(1)详见解析;(2)4![]() .
.
【解析】
(1)由条件可证得四边形CODE为平行四边形,再由菱形的性质可求得∠COD=90°,则可证得四边形CODE为矩形;
(2)首先推知△ABC是等边三角形,所以AC=4,则OC=![]() AC=2,根据勾股定理知
AC=2,根据勾股定理知![]() ,结合矩形的面积公式解答即可.
,结合矩形的面积公式解答即可.
(1)证明:∵CE∥OD,DE∥AC,
∴四边形OCED是平行四边形.
又∵四边形ABCD是菱形,
∴AC⊥BD,即∠COD=90°,
∴四边形OCED是矩形.
(2)解:∵在菱形ABCD中,AB=4,
∴AB=BC=CD=4.
又∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=4,
∴OC=![]() AC=2,
AC=2,
∴![]()
∴矩形OCED的面积是2![]() ×2=4
×2=4![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+![]() x+c经过A(4,0),B(1,0)两点,与y轴交于点C.
x+c经过A(4,0),B(1,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)在直线AC上方的抛物线上是否存在一点D,使得△DCA的面积最大?若存在,求出点D的坐标及△DCA面积的最大值;若不存在,请说明理由.
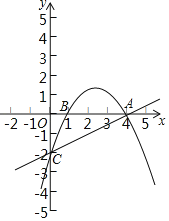
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区九年级学生身体素质情况,该区从全区九年级学生中随机抽取了部分学生进行了一次体育考试科目测试(把测试结果分为四个等级:A级;优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如图两幅不完整的统计图.请根据统计图中的信息解答下列问题:
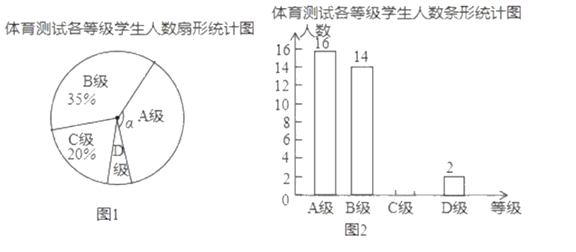
(1)本次抽样测试的学生是__;
(2)求图1中![]() 的度数是
的度数是 ![]() ,把图2条形统计图补充完整;
,把图2条形统计图补充完整;
(3)该区九年级有学生![]() 名,如果全部参加这次体育科目测试,请估计不及格的人数为___.
名,如果全部参加这次体育科目测试,请估计不及格的人数为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
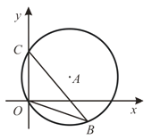
【题目】如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则∠OBC 的余弦值为 _________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,点P、Q分别在BC、CD上,∠PAQ=∠B.
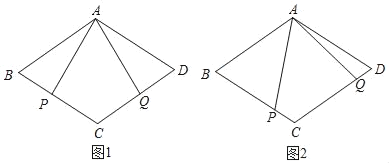
(1)如图1,若AP⊥BC,求证:AP=AQ;
(2)如图2,若点P为BC上一点,AP=AQ仍成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
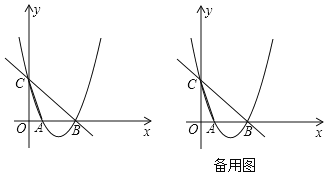
【题目】如图,在平面直角坐标系中,直线y=﹣x+5与x轴交于点B,与y轴交于点C.抛物线y=x2+bx+c经过点B和点C,与x轴交于另一点A,连接AC.
(1)求抛物线的解析式;
(2)若点Q在直线BC上方的抛物线上,连接QC,QB,当△ABC与△QBC的面积比等于2:3时,直接写出点Q的坐标:
(3)在(2)的条件下,点H在x轴的负半轴,连接AQ,QH,当∠AQH=∠ACB时,直接写出点H的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月,北京地铁共“金山银山,不如绿水青山”.某市不断推进“森林城市”建设,今春种植四类树苗,园林部门从种植的这批树苗中随机抽取了4000棵,将各类树苗的种植棵数绘制成扇形统计图,将各类树苗的成活棵数绘制成条形统计图,经统计松树和杨树的成活率较高,且杨树的成活率为97%,根据图表中的信息解答下列问题:
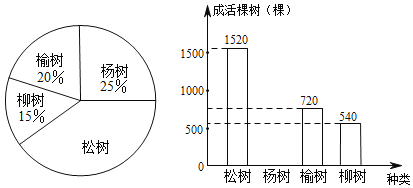
(1)扇形统计图中松树所对的圆心角为 度,并补全条形统计图.
(2)该市今年共种树16万棵,成活了约多少棵?
(3)园林部门决定明年从这四类树苗中选两类种植,请用列表法或树状图求恰好选到成活率较高的两类树苗的概率.(松树、杨树、榆树、柳树分别用A,B,C,D表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
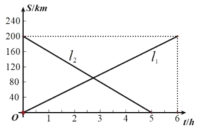
【题目】已知![]() 两地相距
两地相距![]() ,甲、乙两辆货车装满货物分别从
,甲、乙两辆货车装满货物分别从![]() 两地相向而行,图中
两地相向而行,图中![]() 分别表示甲、乙两辆货车离
分别表示甲、乙两辆货车离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数关系.请你根据以上信息,解答下列问题:
之间的函数关系.请你根据以上信息,解答下列问题:
(1)分别求出直线![]() 所对应的函数关系式;
所对应的函数关系式;
(2)何时甲货车离![]() 地的距离大于乙货车离
地的距离大于乙货车离![]() 地的距离?
地的距离?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于两个不相等的实数a,b,我们规定符号max{a,b}表示a、b中的较大的数,如:max{2,4}=4,按照这个规定,方程max{x,﹣x}=x2﹣x﹣1的解为( )
A.1+![]() 或1﹣
或1﹣![]() B.1或﹣1C.1﹣
B.1或﹣1C.1﹣![]() 或1D.1+
或1D.1+![]() 或﹣1
或﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com